La ricompensa è la forza trainante per gli agenti di apprendimento per rinforzo (RL). Dato il suo ruolo centrale nella vita reale, si presume spesso che la ricompensa sia adeguatamente generale nella sua espressività, come riassunto dall’ipotesi della ricompensa di Sutton e Littman:
“…tutto ciò che intendiamo per obiettivi e scopi può essere ben pensato come la massimizzazione del valore atteso della somma cumulativa di un segnale scalare ricevuto (ricompensa).”
– SUTTON (2004), LITTMAN (2017)
Nel nostro lavoro facciamo i primi passi verso uno studio sistematico di questa ipotesi. Per fare ciò, consideriamo il seguente esperimento mentale che coinvolge Alice, una designer, e Bob, un agente di apprendimento:
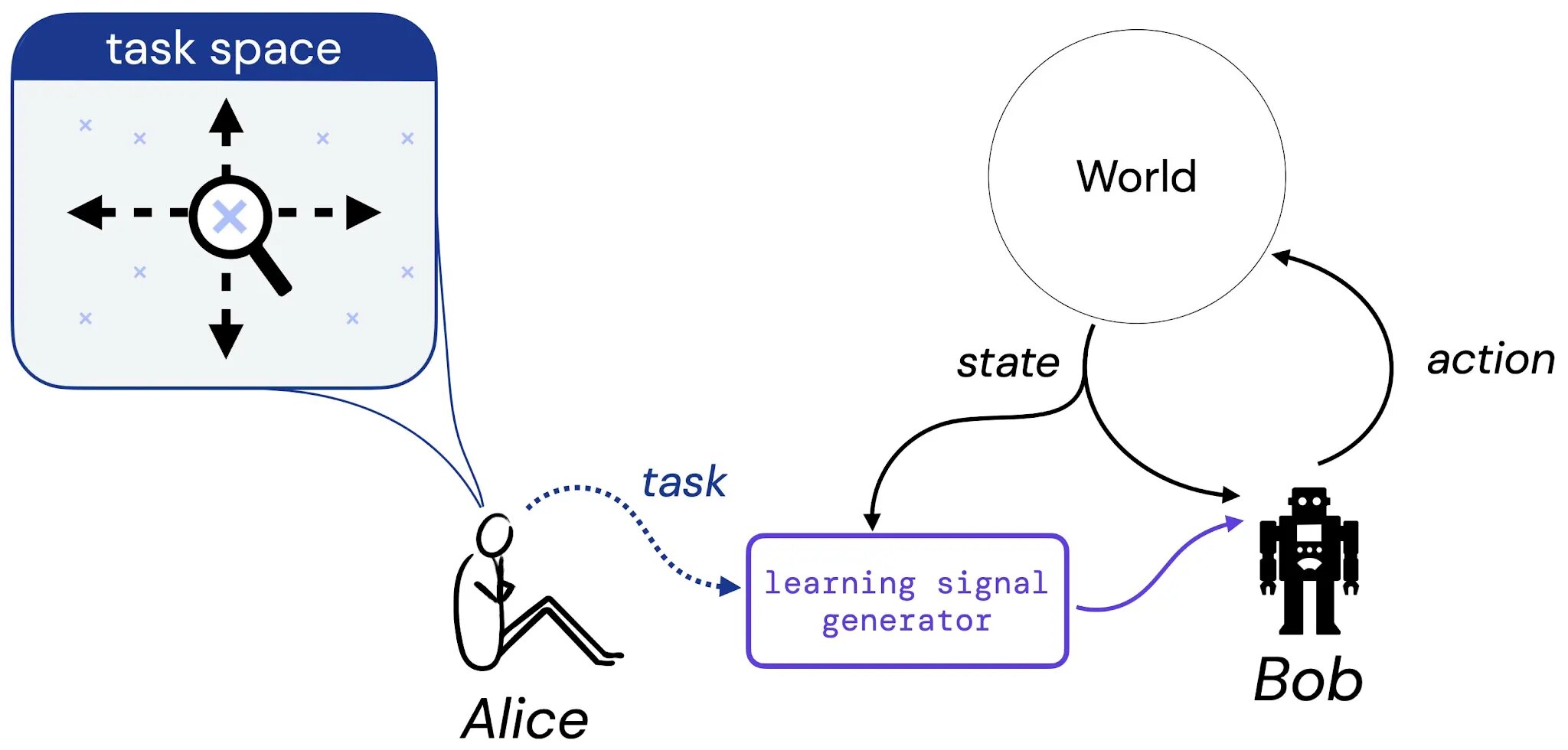
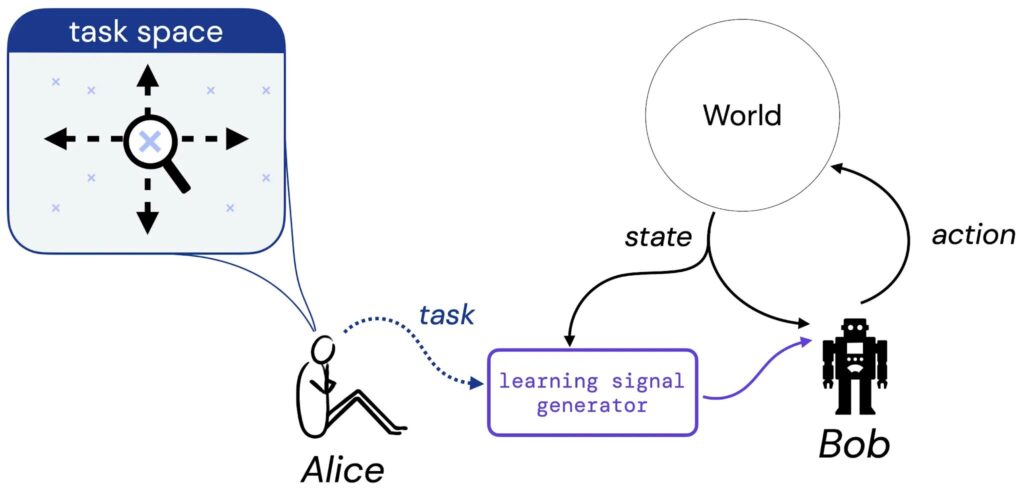
Supponiamo che Alice pensi a un compito che vorrebbe che Bob imparasse a risolvere – questo compito potrebbe essere nella forma di una descrizione in linguaggio naturale (“bilanciare questo polo”), uno stato di cose immaginato (“raggiungere una qualsiasi delle configurazioni vincenti di una scacchiera”), o qualcosa di più tradizionale come una ricompensa o una funzione di valore. Quindi, immaginiamo che Alice traduca la sua scelta di compito in un generatore che fornirà un segnale di apprendimento (come una ricompensa) a Bob (un agente di apprendimento), che imparerà da questo segnale per tutta la sua vita. Successivamente basiamo il nostro studio sull’ipotesi della ricompensa rispondendo alla seguente domanda: data la scelta del compito da parte di Alice, esiste sempre una funzione di ricompensa che può trasferire questo compito a Bob?
Cos’è un compito?
Per rendere concreto il nostro studio su questa questione, limitiamo innanzitutto l’attenzione a tre tipi di compiti. In particolare, introduciamo tre tipi di attività che riteniamo catturino tipi di compiti sensati: 1) Un insieme di politiche accettabili (SOAP), 2) Un ordine politico (PO) e 3) Un ordine di traiettoria (TO). Queste tre forme di compiti rappresentano esempi concreti del tipo di compiti che potremmo volere che un agente impari a risolvere.
.jpg)
Studieremo quindi se la ricompensa è in grado di catturare ciascuno di questi tipi di compiti in ambienti finiti. Fondamentalmente, focalizziamo l’attenzione solo sulle funzioni di ricompensa di Markov; ad esempio, dato uno spazio di stato sufficiente per formare un compito come coppie (x,y) in un mondo a griglia, esiste una funzione di ricompensa che dipende solo da questo stesso spazio di stato che può catturare il compito?
Primo risultato principale
Il nostro primo risultato principale mostra che per ciascuno dei tre tipi di attività esistono coppie ambiente-attività per le quali non esiste una funzione di ricompensa di Markov in grado di catturare l’attività. Un esempio di tale coppia è l’attività “fai il giro completo della griglia in senso orario o antiorario” in un tipico mondo a griglia:
.jpg)
Questo compito è naturalmente catturato da un SOAP che consiste di due politiche accettabili: la politica “in senso orario” (in blu) e la politica “in senso antiorario” (in viola). Affinché una funzione di ricompensa di Markov possa esprimere questo compito, sarebbe necessario rendere queste due politiche strettamente più elevate in termini di valore rispetto a tutte le altre politiche deterministiche. Tuttavia, non esiste una funzione di ricompensa di Markov: l’ottimalità di una singola azione di “muovi in senso orario” dipenderà dal fatto che l’agente si stesse già muovendo in quella direzione in passato. Poiché la funzione di ricompensa deve essere Markov, non può trasmettere questo tipo di informazioni. Esempi simili dimostrano che la ricompensa di Markov non può catturare anche ogni ordine politico e ordine di traiettoria.
Secondo risultato principale
Dato che alcuni compiti possono essere acquisiti e altri no, esploreremo poi se esiste una procedura efficiente per determinare se un dato compito può essere acquisito tramite ricompensa in un dato ambiente. Inoltre, se esiste una funzione di ricompensa che cattura il compito assegnato, idealmente vorremmo essere in grado di produrre tale funzione di ricompensa. Il nostro secondo risultato è un risultato positivo che dice che per qualsiasi coppia finita ambiente-compito, esiste una procedura che può 1) decidere se il compito può essere catturato dalla ricompensa di Markov in un dato ambiente e 2) produrre la funzione di ricompensa desiderata che trasmette esattamente il compito, quando esiste una tale funzione.
Questo lavoro stabilisce percorsi iniziali verso la comprensione della portata dell’ipotesi della ricompensa, ma c’è ancora molto da fare per generalizzare questi risultati oltre gli ambienti finiti, le ricompense di Markov e le semplici nozioni di “compito” ed “espressività”. Ci auguriamo che questo lavoro fornisca nuove prospettive concettuali sulla ricompensa e sul suo posto nell’apprendimento per rinforzo.


