Padroneggiare la segmentazione della clientela con gli LLM | Intelligenza-Artificiale

Questo è il metodo più comune e quello che sicuramente conoscerai. Comunque lo studieremo perché mostrerò tecniche di analisi avanzate in questi casi. Il quaderno Jupyter dove troverete la procedura completa si chiama kmeans.ipynb

Preelaborato

Viene eseguita una preelaborazione delle variabili:

1. Consiste nel convertire le variabili categoriali in variabili numeriche. Possiamo applicare un Onehot Encoder (la solita cosa) ma in questo caso applicheremo un Ordinal Encoder.
2. Cerchiamo di garantire che le variabili numeriche abbiano una distribuzione gaussiana. Per loro applicheremo un PowerTransformer.

Vediamo come appare nel codice.

import pandas as pd # dataframe manipulation
import numpy as np # linear algebra
# data visualization
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import plotly.express as px
import plotly.graph_objects as go
import seaborn as sns
import shap
# sklearn 
from sklearn.cluster import KMeans
from sklearn.preprocessing import PowerTransformer, OrdinalEncoder
from sklearn.pipeline import Pipeline
from sklearn.manifold import TSNE
from sklearn.metrics import silhouette_score, silhouette_samples, accuracy_score, classification_report
from pyod.models.ecod import ECOD
from yellowbrick.cluster import KElbowVisualizer
import lightgbm as lgb
import prince
df = pd.read_csv("train.csv", sep = ";")
df = df.iloc(:, 0:8)
pipe = Pipeline((('ordinal', OrdinalEncoder()), ('scaler', PowerTransformer())))
pipe_fit = pipe.fit(df)
data = pd.DataFrame(pipe_fit.transform(df), columns = df.columns)
data

Produzione:

Valori anomali

È fondamentale che ci siano meno valori anomali nei nostri dati poiché Kmeans è molto sensibile a questo. Possiamo applicare il metodo tipico di scelta dei valori anomali utilizzando il punteggio z, ma in questo post ti mostrerò un metodo molto più avanzato e interessante.

Bene, qual è questo metodo? Bene, useremo il Libreria Python Outlier Detection (PyOD).. Questa libreria è focalizzata sul rilevamento di valori anomali per diversi casi. Per essere più specifici useremo il file ECOD metodo (“funzioni di distribuzione cumulativa empirica per il rilevamento di valori anomali“).

Questo metodo cerca di ottenere la distribuzione dei dati e quindi sapere quali sono i valori in cui la densità di probabilità è inferiore (outlier). Dai un’occhiata a Github se vuoi.

from pyod.models.ecod import ECOD
clf = ECOD()
clf.fit(data)
outliers = clf.predict(data) 
data("outliers") = outliers
# Data without outliers
data_no_outliers = data(data("outliers") == 0)
data_no_outliers = data_no_outliers.drop(("outliers"), axis = 1)
# Data with Outliers
data_with_outliers = data.copy()
data_with_outliers = data_with_outliers.drop(("outliers"), axis = 1)
print(data_no_outliers.shape) -> (40691, 8)
print(data_with_outliers.shape) -> (45211, 8)

Modellazione

Uno degli svantaggi dell’utilizzo dell’algoritmo Kmeans è che devi scegliere il numero di cluster che desideri utilizzare. In questo caso, al fine di ottenere tali dati, utilizzeremo Metodo del gomito. Consiste nel calcolare la distorsione che esiste tra i punti di un ammasso e il suo baricentro. L’obiettivo è chiaro, ottenere la minima distorsione possibile. In questo caso utilizziamo il seguente codice:

from yellowbrick.cluster import KElbowVisualizer
# Instantiate the clustering model and visualizer
km = KMeans(init="k-means++", random_state=0, n_init="auto")
visualizer = KElbowVisualizer(km, k=(2,10))
visualizer.fit(data_no_outliers)        # Fit the data to the visualizer
visualizer.show()    

Produzione:

Lo vediamo da k=5la distorsione non varia drasticamente. È vero che l’ideale è che il comportamento a partire da k= 5 sia quasi piatto. Ciò accade raramente e possono essere applicati altri metodi per essere sicuri del numero ottimale di cluster. A dire il vero, potremmo eseguire a Sagoma visualizzazione. Il codice è il seguente:

from sklearn.metrics import davies_bouldin_score, silhouette_score, silhouette_samples
import matplotlib.cm as cm
def make_Silhouette_plot(X, n_clusters):
plt.xlim((-0.1, 1))
plt.ylim((0, len(X) + (n_clusters + 1) * 10))
clusterer = KMeans(n_clusters=n_clusters, max_iter = 1000, n_init = 10, init = 'k-means++', random_state=10)
cluster_labels = clusterer.fit_predict(X)
silhouette_avg = silhouette_score(X, cluster_labels)
print(
"For n_clusters =", n_clusters,
"The average silhouette_score is :", silhouette_avg,
)
# Compute the silhouette scores for each sample
sample_silhouette_values = silhouette_samples(X, cluster_labels)
y_lower = 10
for i in range(n_clusters):
ith_cluster_silhouette_values = sample_silhouette_values(cluster_labels == i)
ith_cluster_silhouette_values.sort()
size_cluster_i = ith_cluster_silhouette_values.shape(0)
y_upper = y_lower + size_cluster_i
color = cm.nipy_spectral(float(i) / n_clusters)
plt.fill_betweenx(
np.arange(y_lower, y_upper),
0,
ith_cluster_silhouette_values,
facecolor=color,
edgecolor=color,
alpha=0.7,
)
plt.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))
y_lower = y_upper + 10
plt.title(f"The Silhouette Plot for n_cluster = {n_clusters}", fontsize=26)
plt.xlabel("The silhouette coefficient values", fontsize=24)
plt.ylabel("Cluster label", fontsize=24)
plt.axvline(x=silhouette_avg, color="red", linestyle="--")
plt.yticks(())  
plt.xticks((-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1))
range_n_clusters = list(range(2,10))
for n_clusters in range_n_clusters:
print(f"N cluster: {n_clusters}")
make_Silhouette_plot(data_no_outliers, n_clusters)   
plt.savefig('Silhouette_plot_{}.png'.format(n_clusters))
plt.close()
OUTPUT:
"""
N cluster: 2
For n_clusters = 2 The average silhouette_score is : 0.1775761520337095
N cluster: 3
For n_clusters = 3 The average silhouette_score is : 0.20772622268785523
N cluster: 4
For n_clusters = 4 The average silhouette_score is : 0.2038116470937145
N cluster: 5
For n_clusters = 5 The average silhouette_score is : 0.20142888327171368
N cluster: 6
For n_clusters = 6 The average silhouette_score is : 0.20252892716996912
N cluster: 7
For n_clusters = 7 The average silhouette_score is : 0.21185490763840265
N cluster: 8
For n_clusters = 8 The average silhouette_score is : 0.20867816457291538
N cluster: 9
For n_clusters = 9 The average silhouette_score is : 0.21154289421300868
"""

Si può vedere che il punteggio di silhouette più alto si ottiene con n_cluster=9, ma è anche vero che la variazione del punteggio è piuttosto piccola se la confrontiamo con gli altri punteggi. Al momento il risultato precedente non ci fornisce molte informazioni. D’altra parte, il codice precedente crea la visualizzazione Silhouette, che ci fornisce maggiori informazioni:

Poiché comprendere bene queste rappresentazioni non è l’obiettivo di questo post, concluderò che non sembra esserci una decisione molto chiara su quale sia il numero migliore. Dopo aver visionato le rappresentazioni precedenti possiamo scegliere K=5 o K=6. Questo perché per i diversi cluster il punteggio Silhouette è superiore al valore medio e non vi è alcuno squilibrio nella dimensione dei cluster. Inoltre, in alcune situazioni, il reparto marketing potrebbe essere interessato ad avere il minor numero di cluster/tipi di clienti (questo può essere o meno il caso).

Finalmente possiamo creare il nostro modello Kmeans con K=5.

km = KMeans(n_clusters=5,
init='k-means++', 
n_init=10,
max_iter=100, 
random_state=42)
clusters_predict = km.fit_predict(data_no_outliers)
"""
clusters_predict -> array((4, 2, 0, ..., 3, 4, 3))
np.unique(clusters_predict) -> array((0, 1, 2, 3, 4))
"""

Valutazione

Il modo di valutare i modelli kmeans è un po’ più aperto rispetto ad altri modelli. Possiamo usare

• metrica
• visualizzazioni
• interpretazione (Qualcosa di molto importante per le aziende).

In relazione a metriche di valutazione del modellopossiamo usare il seguente codice:

from sklearn.metrics import silhouette_score
from sklearn.metrics import calinski_harabasz_score
from sklearn.metrics import davies_bouldin_score
"""
The Davies Bouldin index is defined as the average similarity measure 
of each cluster with its most similar cluster, where similarity 
is the ratio of within-cluster distances to between-cluster distances.
The minimum value of the DB Index is 0, whereas a smaller 
value (closer to 0) represents a better model that produces better clusters.
"""
print(f"Davies bouldin score: {davies_bouldin_score(data_no_outliers,clusters_predict)}")
"""
Calinski Harabaz Index -> Variance Ratio Criterion.
Calinski Harabaz Index is defined as the ratio of the 
sum of between-cluster dispersion and of within-cluster dispersion.
The higher the index the more separable the clusters.
"""
print(f"Calinski Score: {calinski_harabasz_score(data_no_outliers,clusters_predict)}")
"""
The silhouette score is a metric used to calculate the goodness of 
fit of a clustering algorithm, but can also be used as 
a method for determining an optimal value of k (see here for more).
Its value ranges from -1 to 1.
A value of 0 indicates clusters are overlapping and either
the data or the value of k is incorrect.
1 is the ideal value and indicates that clusters are very 
dense and nicely separated.
"""
print(f"Silhouette Score: {silhouette_score(data_no_outliers,clusters_predict)}")
OUTPUT:
"""
Davies bouldin score: 1.5480952939773156
Calinski Score: 7646.959165727562
Silhouette Score: 0.2013600389183821
"""

Per quanto si può dimostrare, non abbiamo un modello eccessivamente buono. Il punteggio di Davies ci sta dicendo che la distanza tra i cluster è piuttosto piccola.

Ciò può essere dovuto a diversi fattori, ma tieni presente che l’energia di un modello sono i dati; se i dati non hanno sufficiente potere predittivo non si può pretendere di ottenere risultati eccezionali.

Per visualizzazionipossiamo usare il metodo per ridurre dimensionalità, PCA. Per loro useremo il file Principe libreria, focalizzata sull’analisi esplorativa e sulla riduzione della dimensionalità. Se preferisci puoi usare i PCA di Sklearn, sono identici.

Per prima cosa calcoleremo i componenti principali in 3D, poi ne faremo la rappresentazione. Queste sono le due funzioni eseguite dai passaggi precedenti:

import prince
import plotly.express as px
def get_pca_2d(df, predict):
pca_2d_object = prince.PCA(
n_components=2,
n_iter=3,
rescale_with_mean=True,
rescale_with_std=True,
copy=True,
check_input=True,
engine='sklearn',
random_state=42
)
pca_2d_object.fit(df)
df_pca_2d = pca_2d_object.transform(df)
df_pca_2d.columns = ("comp1", "comp2")
df_pca_2d("cluster") = predict
return pca_2d_object, df_pca_2d
def get_pca_3d(df, predict):
pca_3d_object = prince.PCA(
n_components=3,
n_iter=3,
rescale_with_mean=True,
rescale_with_std=True,
copy=True,
check_input=True,
engine='sklearn',
random_state=42
)
pca_3d_object.fit(df)
df_pca_3d = pca_3d_object.transform(df)
df_pca_3d.columns = ("comp1", "comp2", "comp3")
df_pca_3d("cluster") = predict
return pca_3d_object, df_pca_3d
def plot_pca_3d(df, title = "PCA Space", opacity=0.8, width_line = 0.1):
df = df.astype({"cluster": "object"})
df = df.sort_values("cluster")
fig = px.scatter_3d(
df, 
x='comp1', 
y='comp2', 
z='comp3',
color='cluster',
template="plotly",
# symbol = "cluster",
color_discrete_sequence=px.colors.qualitative.Vivid,
title=title).update_traces(
# mode = 'markers',
marker={
"size": 4,
"opacity": opacity,
# "symbol" : "diamond",
"line": {
"width": width_line,
"color": "black",
}
}
).update_layout(
width = 800, 
height = 800, 
autosize = True, 
showlegend = True,
legend=dict(title_font_family="Times New Roman",
font=dict(size= 20)),
scene = dict(xaxis=dict(title = 'comp1', titlefont_color = 'black'),
yaxis=dict(title = 'comp2', titlefont_color = 'black'),
zaxis=dict(title = 'comp3', titlefont_color = 'black')),
font = dict(family = "Gilroy", color  = 'black', size = 15))
fig.show()

Non preoccuparti troppo di queste funzioni, usale come segue:

pca_3d_object, df_pca_3d = pca_plot_3d(data_no_outliers, clusters_predict)
plot_pca_3d(df_pca_3d, title = "PCA Space", opacity=1, width_line = 0.1)
print("The variability is :", pca_3d_object.eigenvalues_summary)

Produzione:

Si può vedere che i cluster non hanno quasi alcuna separazione tra loro e non esiste una divisione chiara. Ciò è in conformità con le informazioni fornite dalle metriche.

Qualcosa da tenere a mente e che pochissime persone tengono a mente è il PCA e il variabilità degli autovettori.

Diciamo che ogni campo contiene una certa quantità di informazioni e questo aggiunge la sua parte di informazione. Se la somma cumulata delle 3 componenti principali ammonta a circa l’80% di variabilità, possiamo dire che è accettabile, ottenendo buoni risultati nelle rappresentazioni. Se il valore è inferiore, dobbiamo prendere le visualizzazioni con le pinze poiché ci mancano molte informazioni contenute in altri autovettori.

La domanda successiva è ovvia: qual è la variabilità della PCA eseguita?

La risposta è la seguente:

Come si può vedere, abbiamo una variabilità del 48,37% con le prime 3 componenti, un dato insufficiente per trarre conclusioni informate.

Si scopre che quando viene eseguita un’analisi PCA, la struttura spaziale non viene preservata. Fortunatamente esiste un metodo meno conosciuto, chiamato t-SNEche ci permette di farlo ridurre la dimensionalità e mantenere anche la struttura spaziale. Questo può aiutarci a visualizzare, poiché con il metodo precedente non abbiamo avuto molto successo.

Se lo provate sui vostri computer tenete presente che ha un costo computazionale maggiore. Per questo motivo ho campionato il mio set di dati originale e mi ci sono voluti circa 5 minuti per ottenere il risultato. Il codice è il seguente:

from sklearn.manifold import TSNE
sampling_data = data_no_outliers.sample(frac=0.5, replace=True, random_state=1)
sampling_clusters = pd.DataFrame(clusters_predict).sample(frac=0.5, replace=True, random_state=1)(0).values
df_tsne_3d = TSNE(
n_components=3, 
learning_rate=500, 
init='random', 
perplexity=200, 
n_iter = 5000).fit_transform(sampling_data)
df_tsne_3d = pd.DataFrame(df_tsne_3d, columns=("comp1", "comp2",'comp3'))
df_tsne_3d("cluster") = sampling_clusters
plot_pca_3d(df_tsne_3d, title = "PCA Space", opacity=1, width_line = 0.1)

Di conseguenza, ho ottenuto la seguente immagine. Mostra una maggiore separazione tra i cluster e ci consente di trarre conclusioni in modo più chiaro.

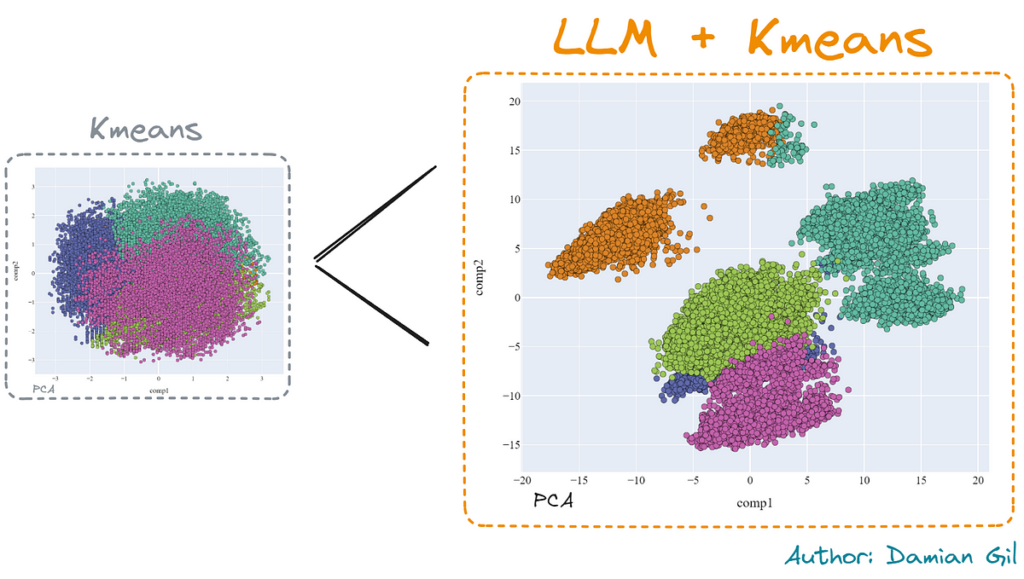
Possiamo infatti paragonare la riduzione operata dal PCA e dal t-SNE, in 2 dimensioni. Il miglioramento è evidente utilizzando il secondo metodo.

Infine, esploriamo un po’ come funziona il modello, in quali caratteristiche sono le più importanti e quali sono le principali caratteristiche dei cluster.

Per vedere l’importanza di ciascuna variabile utilizzeremo un “trucco” tipico di questo tipo di situazione. Creeremo un modello di classificazione in cui la “X” rappresenta gli input del modello Kmeans e la “y” sono i cluster previsti dal modello Kmeans.

Il modello scelto è un LGBMClassificatore. Questo modello è abbastanza potente e funziona bene con variabili categoriche e numeriche. Avere addestrato il nuovo modello, utilizzando il file SHAP libreria, possiamo ottenere l’importanza di ciascuna delle caratteristiche nella previsione. Il codice è:

import lightgbm as lgb
import shap
# We create the LGBMClassifier model and train it
clf_km = lgb.LGBMClassifier(colsample_by_tree=0.8)
clf_km.fit(X=data_no_outliers, y=clusters_predict)
#SHAP values
explainer_km = shap.TreeExplainer(clf_km)
shap_values_km = explainer_km.shap_values(data_no_outliers)
shap.summary_plot(shap_values_km, data_no_outliers, plot_type="bar", plot_size=(15, 10))

Produzione:

Si può vedere quella caratteristica alloggiamento ha il maggior potere predittivo. Si può anche vedere che il cluster numero 4 (verde) è principalmente differenziato da prestito variabile.

Infine dobbiamo analizzare le caratteristiche dei cluster. Questa parte dello studio è decisiva per l’azienda. Per loro otterremo le medie (per le variabili numeriche) e il valore più frequente (variabili categoriali) di ciascuna delle caratteristiche del set di dati per ciascuno dei cluster:

df_no_outliers = df(df.outliers == 0)
df_no_outliers("cluster") = clusters_predict
df_no_outliers.groupby('cluster').agg(
{
'job': lambda x: x.value_counts().index(0),
'marital': lambda x: x.value_counts().index(0),
'education': lambda x: x.value_counts().index(0),
'housing': lambda x: x.value_counts().index(0),
'loan': lambda x: x.value_counts().index(0),
'contact': lambda x: x.value_counts().index(0),
'age':'mean',
'balance': 'mean',
'default': lambda x: x.value_counts().index(0),
}
).reset_index()

Produzione:

Vediamo che i cluster con lavoro=colletto blu non presentano una grande differenziazione tra le loro caratteristiche. Ciò non è auspicabile poiché è difficile differenziare i clienti di ciascuno dei cluster. Nel lavoro=gestione caso, otteniamo una migliore differenziazione.

Dopo aver effettuato l’analisi in modi diversi, convergono alla stessa conclusione: “Dobbiamo migliorare i risultati”.