Algebra lineare 2: forme di matrici Echelon | di tenzin migmar (t9nz) | Settembre 2023 | Intelligenza-Artificiale

Forma a scaglioni di fila e forma a scaglioni di fila ridotta

Prefazione

Bentornati al secondo saggio della mia serie in corso sulle basi dell’algebra lineare, la matematica fondamentale dietro l’apprendimento automatico. Nel mio precedente articoloHo introdotto equazioni e sistemi lineari, notazione matriciale e operazioni di riduzione delle righe. Questo articolo illustrerà le forme della matrice a scaglioni: la forma a scaglioni di riga e la forma a scaglioni ridotta a righe e come entrambe possono essere utilizzate per risolvere sistemi lineari. Questo articolo sarebbe più utile ai lettori se letto insieme a Algebra lineare e le sue applicazioni di David C. Lay, Steven R. Lay e Judi J. McDonald. Considera questa serie come una risorsa complementare esterna.

Sentiti libero di condividere pensieri, domande e critiche.

Modulo a scaglioni di fila

IL Eliminazione di Gauss Il metodo è una procedura per trasformare una matrice utilizzando operazioni sulle righe in una forma in cui le soluzioni possono diventare recuperabili dopo alcune sostituzioni all’indietro.

A titolo di ripasso, le operazioni di riduzione delle righe sono:

1. Sostituzione: “sostituisci una riga con la somma di se stessa e di un’altra riga.”*
2. Scambio: “scambia due righe.”*
3. Ridimensionamento: “moltiplica tutte le voci di una riga per una costante diversa da zero.”*

Le operazioni di cui sopra possono essere applicate a una matrice per trasformare quella matrice nella sua forma a scaglioni di righe. Un dato M X N matrice, dove M è il numero di righe e N è il numero di colonne che si dice siano in fila a scaglioni quando:

1. Tutte le righe in cui tutte le voci sono zero si trovano sotto le righe in cui almeno una voce è diversa da zero.
2. Tutte le voci iniziali di una riga (la prima voce da sinistra diversa da zero) si trovano in una colonna a destra della riga sopra di essa.
3. Tutte le voci in una colonna sotto una voce iniziale sono zero.

Di seguito sono riportati esempi di matrici in forma di scaglioni di righe (REF).

Prendetevi un momento per apprezzare come, sebbene ci siano variazioni nelle dimensioni e nelle voci delle matrici, tutte sono considerate in forma di scaglioni di fila secondo i criteri sopra delineati. Notate il motivo a scala sotto le voci principali evidenziate? Questo è ciò che emerge naturalmente dall’esecuzione dell’eliminazione gaussiana per trasformare una matrice in una forma a scaglioni di righe. La forma ha un nome appropriato: la parola echelon deriva dal francese scaglione che significa piolo di una scala e in seguito venne a significare “gradino”.*

L’idea di base dietro l’eliminazione gaussiana per trasformare una matrice in una forma ridotta per righe è quella di scegliere un pivot (la parola pivot è usata per riferirsi alla voce iniziale: una voce che sarà la prima voce diversa da zero nella sua riga) e poi eliminare tutte le voci sottostanti, azzerando tutto nella colonna sotto il pivot. Per capire perché questo passaggio fa progressi nella trasformazione di una matrice in forma a scaglioni ridotti, rivisitare la definizione della forma a scaglioni ridotta: Nella forma a scaglioni di fila, tutte le voci in una colonna sotto una voce iniziale sono zero. Questo passaggio viene quindi ripetuto nuovamente per ogni riga, ma con cautela! Dobbiamo assicurarci che con ogni selezione di pivot non stiamo violando una delle caratteristiche fondamentali della forma a scaglioni di riga; tutte le voci iniziali di una riga si trovano in una colonna a destra della riga sopra di essa. Tenendo presente questa regola, generalmente è una buona idea iniziare a ruotare attorno alla prima voce nella prima riga e poi procedere lungo le righe da destra a sinistra.

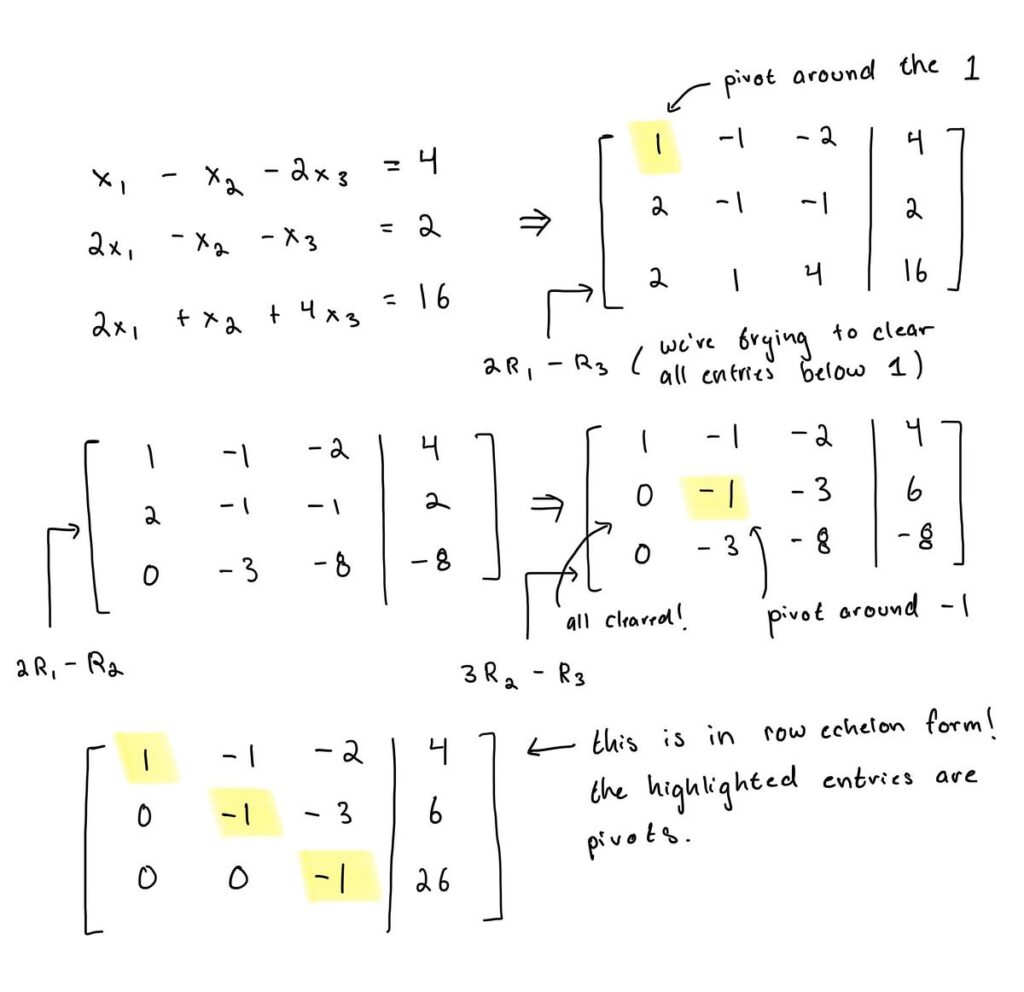
Contempliamo ancora una volta lo scopo della forma a scaglioni di riga menzionata in precedenza: trasformare una data matrice che rappresenta un sistema lineare in una forma in cui le soluzioni possano diventare facilmente leggibili. Per comprendere meglio l’utilità sottostante della forma a scaglioni di riga, considerare l’esempio 1.

Quando eseguiamo l’eliminazione gaussiana, stiamo manipolando la matrice per assumere una forma simmetrica ma più decifrabile. Con la forma a scaglioni di riga ottenuta dall’esempio 1, possiamo ora utilizzare la sostituzione all’indietro per procedere fino a ottenere ciascuna delle soluzioni.

Come puoi vedere dall’alto, questo non è l’ideale. Ci vuole ulteriore lavoro disordinato. Anche lo scaglione di riga ridotto richiede lavoro aggiuntivo, ma la notazione è più pulita e lascia meno spazio agli errori. Una volta ridotta una matrice alla forma a scaglioni di righe ridotte, possiamo facilmente leggere le nostre soluzioni e avremo risolto il sistema lineare.

Forma a scaglioni di fila ridotta

Quando si riduce una matrice a ridotto forma a scaglioni di fila, il Eliminazione di Gauss-Jordan si usa. Questo algoritmo trasforma una data matrice che rappresenta un sistema lineare nella forma a scaglioni ridotti in cui le soluzioni possono diventare facilmente leggibili applicando una serie di operazioni di riduzione delle righe. Non è richiesta alcuna ulteriore sostituzione arretrata.

Un dato M X N Si dice che la matrice sia in forma a scaglioni di righe ridotte se soddisfa i prerequisiti della forma a scaglioni di righe e, inoltre, soddisfa anche i seguenti criteri:

1. Le voci iniziali in ogni riga sono una.
2. Tutte le voci in una colonna sottostante e al di sopra una voce iniziale sono zero. (La voce iniziale è l’unica voce diversa da zero nella colonna)

Analizziamo un esempio di riduzione per righe di una matrice alla forma a scaglioni di righe ridotte.

Leggendo la nostra matrice di forma a scaglioni di righe ridotte, è ora immediatamente ovvio che le nostre soluzioni lo sono x₁ = -3, x₂ = -12, x₃ = -3.

Unicità delle forme Echelon

Finora abbiamo calcolato un esempio ciascuno per la forma a scaglioni di righe e per la forma a scaglioni di righe ridotte. È possibile che tu voglia tentare la riduzione della riga della forma a scaglioni di riga in modo indipendente come esercizio, solo per ritrovarti con una matrice di forma a scaglioni di riga diversa. Non preoccuparti, questo è assolutamente possibile ed entrambe le versioni sono ugualmente corrette purché i calcoli siano stati eseguiti correttamente e tutte e tre le regole siano state coperte. Questa è una situazione fantastica! Ci introduce verso un teorema importante:

Teorema (1)

Le matrici possono avere più di una forma a scaglioni di riga; la forma a scaglioni di riga non è unica. È possibile ottenere forme di scaglioni diverse ma ugualmente valide attraverso variazioni nelle sequenze di come vengono applicate le operazioni sulle righe.

Questo non è il caso della forma a scaglioni a fila ridotta, è il contrario per la forma a scaglioni a fila ridotta.

Teorema (2)

Le matrici devono avere solo una forma a scaglione di riga ridotta; la forma a scaglioni di fila ridotta è unica.

La radice del motivo per cui vediamo questa differenza di unicità tra le due forme è dovuta alle restrizioni aggiuntive che applichiamo alla forma a scaglioni di righe ridotte. Vale a dire, il requisito che le voci iniziali siano pari a uno. Non appena abbiamo ridotto una matrice alla forma a scaglioni di righe, potremmo moltiplicare ciascuna riga per qualsiasi costante diversa da zero e sarebbe ancora nella forma a scaglioni di righe perché il ridimensionamento della matrice non ha infranto alcuna regola per la forma a scaglioni di righe . Lo stesso non è possibile con il modulo a scaglioni ridotti in quanto le voci iniziali devono essere una sola. Illustrerò questo punto più avanti con un esempio concreto.

Numero di soluzioni

Una domanda fondamentale che sorge naturalmente quando si risolve un sistema lineare è: quante soluzioni esistono? Per qualsiasi sistema lineare, la risoluzione sarà sempre uno dei tre casi. Il sistema lineare avrà una soluzione unica, infinite soluzioni o nessuna soluzione. Se sei interessato a riflettere sul perché deve essere uno di questi tre, (ri)visita il mio precedente articolo.

Diamo un’occhiata più da vicino a ciascun caso in modo più dettagliato per vedere come possiamo riconoscere il caso di soluzione di una determinata matrice, e curiosare delicatamente ed esplorare l’intuizione dietro esattamente perché e come si manifesta ogni scenario di caso.

Soluzione Unica: un sistema lineare ha un’unica soluzione quando la forma a scaglioni di righe ridotte della sua matrice ha un perno per ogni colonna.

Diventa più ovvio il motivo per cui questo è il caso quando riscriviamo la forma della matrice come una serie di equazioni lineari. Lo vediamo poiché ogni colonna ha un perno (senza voci sopra o sotto), quindi esiste una soluzione chiara per ogni variabile che puoi leggere equazione per equazione.

Nessuna soluzione: un sistema lineare non ha soluzioni quando la forma a scaglioni di righe ridotte della sua matrice ha un’incoerenza algebrica.

Come visto sopra, non ci sono valori di x₁, x₂, x₃E x₄ ciò consentirà all’equazione quattro di essere vera. Il lato sinistro sarà sempre 0 che non è uguale a nove, quindi non esistono soluzioni per questo sistema. In generale, qualsiasi matrice aumentata con una riga (0, 0, … 0 | B) Dove B è diverso da zero non avrà soluzioni perché 0 ≠ b.

Soluzioni infinite: un sistema lineare ha infinite soluzioni quando ne ha almeno una variabile libera. Una variabile libera si verifica quando la colonna corrispondente non ha un pivot. D’altra parte, a variabile di base è una variabile in cui la colonna corrispondente ha un pivot. Esaminiamo perché la presenza di variabili libere suggerisce infinite soluzioni.

Fedele al suo nome, le variabili libere significano che sei libero di assegnare loro qualsiasi valore. Tutte le variabili di base sono definite rispetto alle variabili libere, quindi i valori delle variabili di base dipenderanno dal valore assegnato alle variabili libere. Questa è l’essenza dell’esistenza di infinite soluzioni; infinite soluzioni sono valide purché le variabili di base siano coerenti con i valori selezionati per le variabili libere.

Dopo aver trasformato una matrice nella forma a scaglioni di righe ridotte, diventerà immediatamente evidente se un sistema ha una, nessuna o infinite soluzioni.

Riepilogo

In questo capitolo abbiamo imparato:

• Il metodo di eliminazione di Gauss per ridurre una matrice alla forma a scaglioni di righe per risolvere un sistema lineare.
• Il metodo di eliminazione di Gauss-Jordan per ridurre una matrice alla forma a scaglioni di righe ridotte per risolvere un sistema lineare.
• Unicità delle forme a scaglioni: la forma a scaglioni di fila non è unica mentre la forma a scaglioni di fila ridotta lo è.
• Il numero di soluzioni che un sistema lineare può avere: uniche, infinite o nessuna e quando e perché si verificano.

Appunti

*Se non diversamente specificato, tutte le immagini sono dell’autore dell’articolo.

*Citazione per le operazioni sulle righe (origine)

*L’etimologia dietro lo scaglione mondiale (src)