In questo pezzo, combino il lavoro precedente sull’accessibilità urbana o sulla pedonabilità con dati open source sulla posizione dei dispositivi defibrillatori pubblici. Inoltre, incorporo i dati sulla popolazione globale e il sistema a griglia H3 di Uber per stimare la percentuale di popolazione ragionevolmente raggiungibile da qualsiasi dispositivo all’interno di Budapest e Vienna.
La radice dell’accessibilità urbana, o pedonabilitàrisiede in un calcolo basato su grafici che misura la distanza euclidea (trasformandola in minuti di cammino, assumendo una velocità costante e l’assenza di ingorghi e ostacoli). I risultati di tali analisi possono dirci quanto sia facile raggiungere specifiche tipologie di servizi da ogni singolo punto della città. Per essere più precisi, da ogni singolo nodo della rete stradale cittadina, ma a causa dell’elevato numero di incroci stradali, questa approssimazione è per lo più trascurabile.
In questo caso di studio, mi concentro su un particolare tipo di punto di interesse (POI): la posizione dei dispositivi defibrillatori. Mentre il portale Open Data del governo austriaco condivide i dati ufficiali al riguardo, in Ungheria ho potuto ottenere solo un set di dati di crowdsourcing con una copertura inferiore alla metà, che, si spera, in seguito crescerà sia in termini di dimensioni assolute che di copertura dei dati.
Nella prima sezione del mio articolo creerò la mappa dell’accessibilità per ogni città, visualizzando il tempo necessario per raggiungere le unità defibrillatrici più vicine entro un raggio di 2,5 km ad una velocità di corsa di 15 km/h. Quindi, dividerò le città in griglie esagonali utilizzando la libreria H3 di Uber per calcolare il tempo medio di accessibilità al defibrillatore per ciascuna cella della griglia. Stimo anche il livello di popolazione in ciascuna cella esagonale seguendo il mio precedente articolo. Infine, li combino e calcolo la frazione della popolazione raggiungibile in funzione del tempo di raggiungibilità (di esecuzione).
Come disclaimer, desidero sottolineare che non sono in alcun modo un esperto medico qualificato e non intendo prendere posizione sull’importanza dei dispositivi defibrillatori rispetto ad altri mezzi di vita supporto. Tuttavia, basandomi sul buon senso e sui principi di pianificazione urbana, suppongo che quanto più facile è raggiungere tali dispositivi, tanto meglio.
Come sempre, mi piace iniziare esplorando i tipi di dati che utilizzo. Per prima cosa raccoglierò i confini amministrativi delle città in cui studio: Budapest, Ungheria e Vienna, Austria.
Quindi, basandosi su un mio articolo precedente su come elaborare i dati sulla popolazione rasterizzati, aggiungo informazioni sulla popolazione a livello di città dall’hub WorldPop. Infine, incorporo i dati governativi ufficiali sui dispositivi defibrillatori a Vienna e la mia versione web degli stessi, sebbene fonti affollate e intrinsecamente incomplete, per Budapest.
1.1. Confini amministrativi
Innanzitutto, interrogo i confini amministrativi di Budapest e Vienna da OpenStreetMap usando il OSMNx biblioteca:
import osmnx as ox # version: 1.0.1
import matplotlib.pyplot as plt # version: 3.7.1admin = {}
cities = ('Budapest', 'Vienna')
f, ax = plt.subplots(1,2, figsize = (15,5))
# visualize the admin boundaries
for idx, city in enumerate(cities):
admin(city) = ox.geocode_to_gdf(city)
admin(city).plot(ax=ax(idx),color='none',edgecolor= 'k', linewidth = 2) ax(idx).set_title(city, fontsize = 16)
Il risultato di questo blocco di codice:
1.2. Dati sulla popolazione
In secondo luogo, seguendo i passaggi in this articoloHo creato la griglia della popolazione in formato dati vettoriali per entrambe le città, basandomi sul database demografico online WorldPop. Senza ripetere i passaggi, ho semplicemente letto i file di output di quel processo contenenti informazioni sulla popolazione di queste città.
Inoltre, per rendere le cose più belle, ho creato una mappa dei colori dal colore del 2022, Very Peri, utilizzando Matplotlib e un rapido script da ChatGPT.
import matplotlib.pyplot as plt
from matplotlib.colors import LinearSegmentedColormapvery_peri = '#8C6BF3'
second_color = '#6BAB55'
colors = (second_color, very_peri )
n_bins = 100
cmap_name = "VeryPeri"
colormap = LinearSegmentedColormap.from_list(cmap_name, colors, N=n_bins)
import geopandas as gpd # version: 0.9.0demographics = {}
f, ax = plt.subplots(1,2, figsize = (15,5))
for idx, city in enumerate(cities):
demographics(city) = gpd.read_file(city.lower() + \
'_population_grid.geojson')(('population', 'geometry'))
admin(city).plot(ax=ax(idx), color = 'none', edgecolor = 'k', \
linewidth = 3)
demographics(city).plot(column = 'population', cmap = colormap, \
ax=ax(idx), alpha = 0.9, markersize = 0.25)
ax(idx).set_title(city)
ax(idx).set_title('Population density\n in ' + city, fontsize = 16)
ax(idx).axis('off')
Il risultato di questo blocco di codice:
1.3. Posizioni del defibrillatore
In terzo luogo, ho raccolto dati sulla localizzazione dei defibrillatori disponibili in entrambe le città.
Per Vienna, ho scaricato questo set di dati da portale open data ufficiale del governo austriaco contenente la posizione del punto di 1044 unità:
Sebbene a Budapest/Ungheria non esista un portale open data ufficiale, la Fondazione nazionale ungherese per il cuore ne gestisce uno sito web in crowdsourcing dove gli operatori possono aggiornare la posizione delle loro unità defibrillatori. Il loro database nazionale è composto da 677 unità; tuttavia, il loro disclaimer afferma che conoscono almeno un migliaio di unità operative nel paese e stanno aspettando che i proprietari le carichino. Con un semplice web crawler, ho scaricato la posizione di ciascuna delle 677 unità registrate e ho filtrato i dati impostati su quelli di Budapest, ottenendo un insieme di 148 unità.
# parse the data for each city
gdf_units= {}gdf_units('Vienna') = gpd.read_file('DEFIBRILLATOROGD')
gdf_units('Budapest') = gpd.read_file('budapest_defibrillator.geojson')
for city in cities:
gdf_units(city) = gpd.overlay(gdf_units(city), admin(city))
# visualize the units
f, ax = plt.subplots(1,2, figsize = (15,5))
for idx, city in enumerate(cities):
admin(city).plot(ax=ax(idx),color='none',edgecolor= 'k', linewidth = 3)
gdf_units(city).plot( ax=ax(idx), alpha = 0.9, color = very_peri, \
markersize = 6.0)
ax(idx).set_title('Locations of defibrillator\ndevices in ' + city, \
fontsize = 16)
ax(idx).axis('off')
Il risultato di questo blocco di codice:
Successivamente, ho concluso questo fantastico articolo scritto da Nick Jones nel 2018 su come calcolare l’accessibilità pedonale:
import os
import pandana # version: 0.6
import pandas as pd # version: 1.4.2
import numpy as np # version: 1.22.4
from shapely.geometry import Point # version: 1.7.1
from pandana.loaders import osmdef get_city_accessibility(admin, POIs):
# walkability parameters
walkingspeed_kmh = 15
walkingspeed_mm = walkingspeed_kmh * 1000 / 60
distance = 2500
# bounding box as a list of llcrnrlat, llcrnrlng, urcrnrlat, urcrnrlng
minx, miny, maxx, maxy = admin.bounds.T(0).to_list()
bbox = (miny, minx, maxy, maxx)
# setting the input params, going for the nearest POI
num_pois = 1
num_categories = 1
bbox_string = '_'.join((str(x) for x in bbox))
net_filename = 'data/network_{}.h5'.format(bbox_string)
if not os.path.exists('data'): os.makedirs('data')
# precomputing nework distances
if os.path.isfile(net_filename):
# if a street network file already exists, just load the dataset from that
network = pandana.network.Network.from_hdf5(net_filename)
method = 'loaded from HDF5'
else:
# otherwise, query the OSM API for the street network within the specified bounding box
network = osm.pdna_network_from_bbox(bbox(0), bbox(1), bbox(2), bbox(3))
method = 'downloaded from OSM'
# identify nodes that are connected to fewer than some threshold of other nodes within a given distance
lcn = network.low_connectivity_nodes(impedance=1000, count=10, imp_name='distance')
network.save_hdf5(net_filename, rm_nodes=lcn) #remove low-connectivity nodes and save to h5
# precomputes the range queries (the reachable nodes within this maximum distance)
# so, as long as you use a smaller distance, cached results will be used
network.precompute(distance + 1)
# compute accessibilities on POIs
pois = POIs.copy()
pois('lon') = pois.geometry.apply(lambda g: g.x)
pois('lat') = pois.geometry.apply(lambda g: g.y)
pois = pois.drop(columns = ('geometry'))
network.init_pois(num_categories=num_categories, max_dist=distance, max_pois=num_pois)
network.set_pois(category='all', x_col=pois('lon'), y_col=pois('lat'))
# searches for the n nearest amenities (of all types) to each node in the network
all_access = network.nearest_pois(distance=distance, category='all', num_pois=num_pois)
# transform the results into a geodataframe
nodes = network.nodes_df
nodes_acc = nodes.merge(all_access((1)), left_index = True, right_index = True).rename(columns = {1 : 'distance'})
nodes_acc('time') = nodes_acc.distance / walkingspeed_mm
xs = list(nodes_acc.x)
ys = list(nodes_acc.y)
nodes_acc('geometry') = (Point(xs(i), ys(i)) for i in range(len(xs)))
nodes_acc = gpd.GeoDataFrame(nodes_acc)
nodes_acc = gpd.overlay(nodes_acc, admin)
nodes_acc(('time', 'geometry')).to_file(city + '_accessibility.geojson', driver = 'GeoJSON')
return nodes_acc(('time', 'geometry'))
accessibilities = {}
for city in cities:
accessibilities(city) = get_city_accessibility(admin(city), gdf_units(city))
for city in cities:
print('Number of road network nodes in ' + \
city + ': ' + str(len(accessibilities(city))))
Questo blocco di codice restituisce il numero di nodi della rete stradale a Budapest (116.056) e Vienna (148.212).
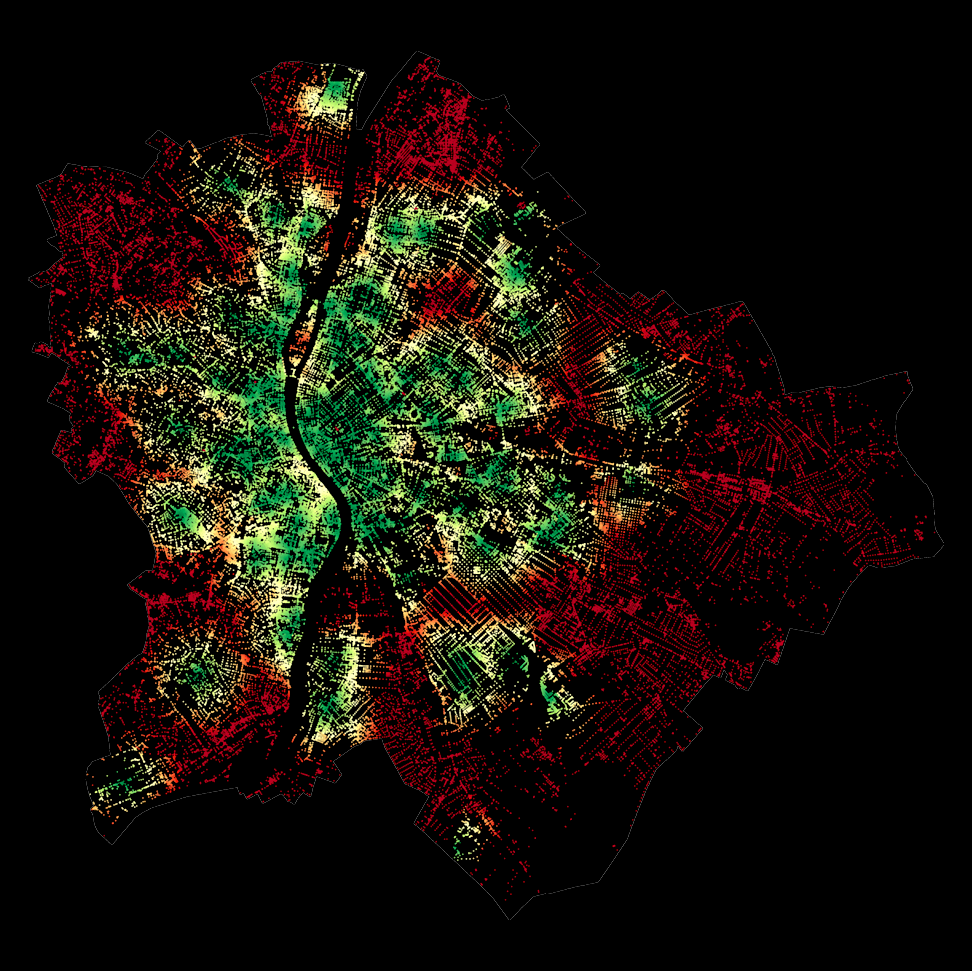
Ora visualizza le mappe di accessibilità:
for city in cities:
f, ax = plt.subplots(1,1,figsize=(15,8))
admin(city).plot(ax=ax, color = 'k', edgecolor = 'k', linewidth = 3)
accessibilities(city).plot(column = 'time', cmap = 'RdYlGn_r', \
legend = True, ax = ax, markersize = 2, alpha = 0.5)
ax.set_title('Defibrillator accessibility in minutes\n' + city, \
pad = 40, fontsize = 24)
ax.axis('off')
Questo blocco di codice restituisce le seguenti cifre:
A questo punto ho sia i dati sulla popolazione che quelli sull’accessibilità; Devo solo metterli insieme. L’unico trucco è che le loro unità spaziali differiscono:
- L’accessibilità viene misurata e collegata a ciascun nodo della rete stradale di ciascuna città
- I dati sulla popolazione derivano da una griglia raster, ora descritta dal POI del centroide di ciascuna griglia raster
Anche se ripristinare la griglia raster originale può essere un’opzione, nella speranza di un’universalità più pronunciata (e aggiungendo un po’ del mio gusto personale), ora mappo questi due tipi di set di dati puntuali nel file Sistema a griglia H3 di Uber per chi non lo ha mai utilizzato, per ora, è sufficiente sapere che si tratta di un elegante ed efficiente sistema di indicizzazione spaziale che utilizza tessere esagonali. E per ulteriori letture, clicca su questo link!
3.1. Creazione di cellule H3
Innanzitutto, metti insieme una funzione che divida una città in esagoni a qualsiasi risoluzione:
import geopandas as gpd
import h3 # version: 3.7.3
from shapely.geometry import Polygon # version: 1.7.1
import numpy as npdef split_admin_boundary_to_hexagons(admin_gdf, resolution):
coords = list(admin_gdf.geometry.to_list()(0).exterior.coords)
admin_geojson = {"type": "Polygon", "coordinates": (coords)}
hexagons = h3.polyfill(admin_geojson, resolution, \
geo_json_conformant=True)
hexagon_geometries = {hex_id : Polygon(h3.h3_to_geo_boundary(hex_id, \
geo_json=True)) for hex_id in hexagons}
return gpd.GeoDataFrame(hexagon_geometries.items(), columns = ('hex_id', 'geometry'))
resolution = 8
hexagons_gdf = split_admin_boundary_to_hexagons(admin(city), resolution)
hexagons_gdf.plot()
Il risultato di questo blocco di codice:
Ora, vedi alcune diverse risoluzioni:
for resolution in (7,8,9):admin_h3 = {}
for city in cities:
admin_h3(city) = split_admin_boundary_to_hexagons(admin(city), resolution)
f, ax = plt.subplots(1,2, figsize = (15,5))
for idx, city in enumerate(cities):
admin(city).plot(ax=ax(idx), color = 'none', edgecolor = 'k', \
linewidth = 3)
admin_h3(city).plot( ax=ax(idx), alpha = 0.8, edgecolor = 'k', \
color = 'none')
ax(idx).set_title(city + ' (resolution = '+str(resolution)+')', \
fontsize = 14)
ax(idx).axis('off')
Il risultato di questo blocco di codice:
Manteniamo la risoluzione 9!
3.2. Mappa i valori nelle celle h3
Ora, ho entrambe le nostre città in un formato a griglia esagonale. Successivamente, mapperò la popolazione e i dati di accessibilità nelle celle esagonali in base alle celle della griglia in cui rientra ciascuna geometria del punto. Per questo, la funzione sjoin di GeoPandasa, che realizza una bella giunzione spaziale, è una buona scelta.
Inoltre, poiché abbiamo più di 100.000 nodi della rete stradale in ogni città e migliaia di centroidi della griglia della popolazione, molto probabilmente ci saranno più PDI mappati in ciascuna cella della griglia esagonale. Sarà quindi necessaria l’aggregazione. Poiché la popolazione è una quantità additiva, aggregherò i livelli di popolazione all’interno dello stesso esagono sommandoli. Tuttavia, l’accessibilità non è estesa, quindi calcolerei invece il tempo medio di accessibilità del defibrillatore per ciascun riquadro.
demographics_h3 = {}
accessibility_h3 = {}for city in cities:
# do the spatial join, aggregate on the population level of each \
# hexagon, and then map these population values to the grid ids
demographics_dict = gpd.sjoin(admin_h3(city), demographics(city)).groupby(by = 'hex_id').sum('population').to_dict()('population')
demographics_h3(city) = admin_h3(city).copy()
demographics_h3(city)('population') = demographics_h3(city).hex_id.map(demographics_dict)
# do the spatial join, aggregate on the population level by averaging
# accessiblity times within each hexagon, and then map these time score # to the grid ids
accessibility_dict = gpd.sjoin(admin_h3(city), accessibilities(city)).groupby(by = 'hex_id').mean('time').to_dict()('time')
accessibility_h3(city) = admin_h3(city).copy()
accessibility_h3(city)('time') = \
accessibility_h3(city).hex_id.map(accessibility_dict)
# now show the results
f, ax = plt.subplots(2,1,figsize = (15,15))
demographics_h3(city).plot(column = 'population', legend = True, \
cmap = colormap, ax=ax(0), alpha = 0.9, markersize = 0.25)
accessibility_h3(city).plot(column = 'time', cmap = 'RdYlGn_r', \
legend = True, ax = ax(1))
ax(0).set_title('Population level\n in ' + city, fontsize = 16)
ax(1).set_title('Defibrillator reachability time\n in ' + city, \
fontsize = 16)
for ax_i in ax: ax_i.axis('off')
I risultati di questo blocco di codice sono le seguenti figure:
In questa fase finale, stimerò la frazione della popolazione raggiungibile dall’unità defibrillatore più vicina entro un certo periodo di tempo. Qui mi baso ancora sul ritmo di corsa relativamente veloce di 15 km/h e sul limite di distanza di 2,5 km.
Dal punto di vista tecnico, unisco la popolazione di livello H3 e i dati temporali di accessibilità e quindi eseguo una semplice soglia sulla dimensione temporale e una somma sulla dimensione della popolazione.
f, ax = plt.subplots(1,2, figsize = (15,5))for idx, city in enumerate(cities):
total_pop = demographics_h3(city).population.sum()
merged = demographics_h3(city).merge(accessibility_h3(city).drop(columns =\
('geometry')), left_on = 'hex_id', right_on = 'hex_id')
time_thresholds = range(10)
population_reached = (100*merged(merged.time<limit).population.sum()/total_pop for limit in time_thresholds)
ax(idx).plot(time_thresholds, population_reached, linewidth = 3, \
color = very_peri)
ax(idx).set_xlabel('Reachability time (min)', fontsize = 14, \
labelpad = 12)
ax(idx).set_ylabel('Fraction of population reached (%)', fontsize = 14, labelpad = 12)
ax(idx).set_xlim((0,10))
ax(idx).set_ylim((0,100))
ax(idx).set_title('Fraction of population vs defibrillator\naccessibility in ' + city, pad = 20, fontsize = 16)
Il risultato di questo blocco di codice sono le seguenti figure:
Nell’interpretare questi risultati, vorrei sottolineare che, da un lato, l’accessibilità del defibrillatore potrebbe non essere direttamente collegata al tasso di sopravvivenza all’infarto; giudicare tale effetto va oltre sia la mia esperienza che lo scopo di questo progetto. Inoltre, i dati utilizzati per Budapest provengono da fonti consapevolmente incomplete e affollate, a differenza della fonte dati ufficiale austriaca.
Dopo i disclaimer, cosa vediamo? Da un lato vediamo che a Budapest circa il 75–80% della popolazione riesce ad accedere ad un apparecchio in 10 minuti, mentre a Vienna raggiungiamo una copertura quasi completa già in circa 6–7 minuti. Inoltre, dobbiamo leggere attentamente questi valori di tempo: se ci capita di trovarci di fronte ad uno sfortunato incidente, dobbiamo raggiungere il dispositivo, ritirarlo, tornare indietro (facendo il tempo di viaggio doppio del tempo di raggiungibilità), installarlo, ecc. in una situazione in cui ogni minuto può essere una questione di vita o di morte.
Quindi, dal punto di vista dello sviluppo, i suggerimenti sono garantire di disporre di dati completi e quindi utilizzare l’accessibilità e le mappe della popolazione, combinarle, analizzarle e basarsi su di esse quando si distribuiscono nuovi dispositivi e nuove posizioni per massimizzare la popolazione effettiva raggiunta .
Fonte: towardsdatascience.com


