Migliora le prestazioni delle previsioni delle serie temporali con una tecnica derivante dall’elaborazione del segnale
La modellazione dei dati delle serie temporali e la loro previsione sono argomenti complessi. Esistono molte tecniche che potrebbero essere utilizzate per migliorare le prestazioni del modello per un lavoro di previsione. Discuteremo qui una tecnica che potrebbe migliorare il modo in cui i modelli di previsione assorbono e utilizzano le caratteristiche temporali e generalizzano da esse. L’obiettivo principale sarà la creazione delle funzionalità stagionali che alimentano il modello di previsione delle serie temporali durante l’addestramento: è possibile ottenere facili vantaggi se si include la trasformata di Fourier nel processo di creazione delle funzionalità.
Questo articolo presuppone che tu abbia familiarità con gli aspetti di base della previsione delle serie temporali: non discuteremo questo argomento in generale, ma solo un perfezionamento di un suo aspetto. Per un’introduzione alla previsione delle serie temporali, vedere il corso Kaggle su questo argomento: la tecnica discussa qui si basa sulla loro lezione sulla stagionalità.
Prendere in considerazione il set di dati trimestrale sulla produzione del cemento Portland australianoche mostra la produzione trimestrale totale di cemento Portland in Australia (in milioni di tonnellate) dal 1956:Q1 al 2014:Q1.
df = pd.read_csv('Quarterly_Australian_Portland_Cement_production_776_10.csv', usecols=('time', 'value'))
# convert time from year float to a proper datetime format
df('time') = df('time').apply(lambda x: str(int(x)) + '-' + str(int(1 + 12 * (x % 1))).rjust(2, '0'))
df('time') = pd.to_datetime(df('time'))
df = df.set_index('time').to_period()
df.rename(columns={'value': 'production'}, inplace=True)
production
time
1956Q1 0.465
1956Q2 0.532
1956Q3 0.561
1956Q4 0.570
1957Q1 0.529
... ...
2013Q1 2.049
2013Q2 2.528
2013Q3 2.637
2013Q4 2.565
2014Q1 2.229(233 rows x 1 columns)
Si tratta di dati di serie temporali con una tendenza, componenti stagionali e altri attributi. Le osservazioni vengono effettuate trimestralmente e abbracciano diversi decenni. Diamo prima un’occhiata ai componenti stagionali, utilizzando il grafico del periodogramma (tutto il codice è incluso nel taccuino associato, collegato alla fine).
Il periodogramma mostra la densità di potenza delle componenti spettrali (componenti stagionali). La componente più forte è quella con durata pari a 4 trimestri, ovvero 1 anno. Ciò conferma l’impressione visiva che le variazioni su e giù più forti nel grafico si verificano circa 10 volte ogni decennio. C’è anche una componente con un periodo di 2 quarti: è lo stesso fenomeno stagionale, e significa semplicemente che la periodicità di 4 quarti non è una semplice onda sinusoidale, ma ha una forma più complessa. Per semplicità ignoreremo i componenti con periodi superiori a 4.
Se si tenta di adattare un modello a questi dati, magari per prevedere la produzione di cemento per tempi successivi alla fine del set di dati, sarebbe una buona idea catturare questa stagionalità annuale in una caratteristica o in un insieme di caratteristiche e fornire quelle al modello in formazione. Vediamo un esempio.
I componenti stagionali possono essere modellati in diversi modi. Spesso sono rappresentati come manichini temporali o come coppie seno-coseno. Si tratta di caratteristiche sintetiche con un periodo pari alla stagionalità che stai tentando di modellare o a un suo sottomultiplo.
Dummy annuali:
seasonal_year = DeterministicProcess(index=df.index, constant=False, seasonal=True).in_sample()
print(seasonal_year)
s(1,4) s(2,4) s(3,4) s(4,4)
time
1956Q1 1.0 0.0 0.0 0.0
1956Q2 0.0 1.0 0.0 0.0
1956Q3 0.0 0.0 1.0 0.0
1956Q4 0.0 0.0 0.0 1.0
1957Q1 1.0 0.0 0.0 0.0
... ... ... ... ...
2013Q1 1.0 0.0 0.0 0.0
2013Q2 0.0 1.0 0.0 0.0
2013Q3 0.0 0.0 1.0 0.0
2013Q4 0.0 0.0 0.0 1.0
2014Q1 1.0 0.0 0.0 0.0(233 rows x 4 columns)
Coppie seno-coseno annuali:
cfr = CalendarFourier(freq='Y', order=2)
seasonal_year_trig = DeterministicProcess(index=df.index, seasonal=False, additional_terms=(cfr)).in_sample()
with pd.option_context('display.max_columns', None, 'display.expand_frame_repr', False):
print(seasonal_year_trig)
sin(1,freq=A-DEC) cos(1,freq=A-DEC) sin(2,freq=A-DEC) cos(2,freq=A-DEC)
time
1956Q1 0.000000 1.000000 0.000000 1.000000
1956Q2 0.999963 0.008583 0.017166 -0.999853
1956Q3 0.017166 -0.999853 -0.034328 0.999411
1956Q4 -0.999963 -0.008583 0.017166 -0.999853
1957Q1 0.000000 1.000000 0.000000 1.000000
... ... ... ... ...
2013Q1 0.000000 1.000000 0.000000 1.000000
2013Q2 0.999769 0.021516 0.043022 -0.999074
2013Q3 0.025818 -0.999667 -0.051620 0.998667
2013Q4 -0.999917 -0.012910 0.025818 -0.999667
2014Q1 0.000000 1.000000 0.000000 1.000000(233 rows x 4 columns)
I manichini temporali possono catturare forme d’onda molto complesse del fenomeno stagionale. D’altra parte, se il periodo è N, allora avrai bisogno di N tempi fittizi, quindi, se il periodo è molto lungo, avrai bisogno di molte colonne fittizie, il che potrebbe non essere desiderabile. Per i modelli non penalizzati, spesso vengono utilizzati solo dummy N-1: uno viene eliminato per evitare problemi di collinearità (lo ignoreremo qui).
Le coppie seno/coseno possono modellare periodi di tempo arbitrariamente lunghi. Ciascuna coppia modellerà una forma d’onda sinusoidale pura con una fase iniziale. Man mano che la forma d’onda della funzione stagionale diventa più complessa, sarà necessario aggiungere più coppie (aumentare l’ordine dell’output da CalendarFourier).
(Nota a margine: utilizziamo una coppia seno/coseno per ogni periodo che vogliamo modellare. Ciò che realmente vogliamo è solo una colonna di A*sin(2*pi*t/T + phi) Dove A è il peso assegnato dal modello alla colonna, t è l’indice temporale della serie e T è il periodo componente. Ma il modello non può correggere la fase iniziale phi durante l’adattamento dei dati: i valori del seno sono precalcolati. Fortunatamente, la formula sopra è equivalente a: A1*sin(2*pi*t/T) + A2*cos(2*pi*t/T) e il modello deve solo trovare i pesi A1 e A2.)
TLDR: Ciò che queste due tecniche hanno in comune è che rappresentano la stagionalità tramite una serie di caratteristiche ripetitive, con valori che si ripetono ciclicamente una volta per il periodo di tempo modellato (manichini temporali e la coppia base seno/coseno) o diversi volte per periodo (seno/coseno di ordine superiore). E ognuna di queste caratteristiche ha valori che variano all’interno di un intervallo fisso: da 0 a 1, o da -1 a 1. Queste sono tutte le caratteristiche di cui abbiamo bisogno per modellare la stagionalità qui.
Vediamo cosa succede quando adattiamo un modello lineare a tali caratteristiche stagionali. Ma prima dobbiamo aggiungere le funzionalità di tendenza alla raccolta di funzionalità utilizzata per addestrare il modello.
Creiamo caratteristiche di tendenza e poi uniamole con i manichini temporali season_year generati sopra:
trend_order = 2
trend_year = DeterministicProcess(index=df.index, constant=True, order=trend_order).in_sample()
X = trend_year.copy()
X = X.join(seasonal_year)
const trend trend_squared s(1,4) s(2,4) s(3,4) s(4,4)
time
1956Q1 1.0 1.0 1.0 1.0 0.0 0.0 0.0
1956Q2 1.0 2.0 4.0 0.0 1.0 0.0 0.0
1956Q3 1.0 3.0 9.0 0.0 0.0 1.0 0.0
1956Q4 1.0 4.0 16.0 0.0 0.0 0.0 1.0
1957Q1 1.0 5.0 25.0 1.0 0.0 0.0 0.0
... ... ... ... ... ... ... ...
2013Q1 1.0 229.0 52441.0 1.0 0.0 0.0 0.0
2013Q2 1.0 230.0 52900.0 0.0 1.0 0.0 0.0
2013Q3 1.0 231.0 53361.0 0.0 0.0 1.0 0.0
2013Q4 1.0 232.0 53824.0 0.0 0.0 0.0 1.0
2014Q1 1.0 233.0 54289.0 1.0 0.0 0.0 0.0(233 rows x 7 columns)
Questo è il dataframe X (funzionalità) che verrà utilizzato per addestrare/convalidare il modello. Stiamo modellando i dati con caratteristiche di tendenza quadratiche, più i 4 manichini temporali necessari per la stagionalità annuale. Il dataframe y (obiettivo) sarà solo i numeri di produzione del cemento.
Ritagliamo un set di validazione dai dati, contenente le osservazioni dell’anno 2010. Adatteremo un modello lineare sulle caratteristiche X mostrate sopra e sull’obiettivo y rappresentato dalla produzione di cemento (la porzione di prova), quindi valuteremo le prestazioni del modello in fase di validazione. Faremo tutto quanto sopra anche con un modello di sola tendenza che si adatterà solo alle caratteristiche della tendenza ma ignorerà la stagionalità.
def do_forecast(X, index_train, index_test, trend_order):
X_train = X.loc(index_train)
X_test = X.loc(index_test)y_train = df('production').loc(index_train)
y_test = df('production').loc(index_test)
model = LinearRegression(fit_intercept=False)
_ = model.fit(X_train, y_train)
y_fore = pd.Series(model.predict(X_test), index=index_test)
y_past = pd.Series(model.predict(X_train), index=index_train)
trend_columns = X_train.columns.to_list()(0 : trend_order + 1)
model_trend = LinearRegression(fit_intercept=False)
_ = model_trend.fit(X_train(trend_columns), y_train)
y_trend_fore = pd.Series(model_trend.predict(X_test(trend_columns)), index=index_test)
y_trend_past = pd.Series(model_trend.predict(X_train(trend_columns)), index=index_train)
RMSLE = mean_squared_log_error(y_test, y_fore, squared=False)
print(f'RMSLE: {RMSLE}')
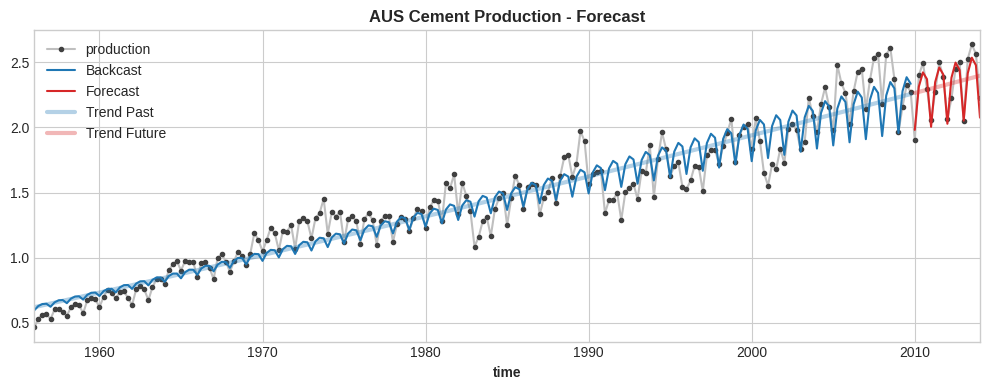
ax = df.plot(**plot_params, title='AUS Cement Production - Forecast')
ax = y_past.plot(color='C0', label='Backcast')
ax = y_fore.plot(color='C3', label='Forecast')
ax = y_trend_past.plot(ax=ax, color='C0', linewidth=3, alpha=0.333, label='Trend Past')
ax = y_trend_fore.plot(ax=ax, color='C3', linewidth=3, alpha=0.333, label='Trend Future')
_ = ax.legend()
do_forecast(X, index_train, index_test, trend_order)
RMSLE: 0.03846449744356434
Il blu è il treno, il rosso è la convalida. Il modello completo è la linea affilata e sottile. Il modello di tendenza è la linea ampia e sfocata.
Questo non è male, ma c’è un problema evidente: il modello ha appreso una stagionalità annuale di ampiezza costante. Anche se la variazione annuale in realtà aumenta nel tempo, il modello può attenersi solo a variazioni di ampiezza fissa. Ovviamente, questo è dovuto al fatto che abbiamo fornito al modello solo caratteristiche stagionali ad ampiezza fissa e non c’è nient’altro nelle caratteristiche (ritardi target, ecc.) per aiutarlo a superare questo problema.
Esaminiamo più a fondo il segnale (i dati) per vedere se c’è qualcosa che potrebbe aiutare con il problema dell’ampiezza fissa.
Il periodogramma evidenzierà tutte le componenti spettrali nel segnale (tutte le componenti stagionali nei dati) e fornirà una panoramica della loro forza complessiva, ma è un aggregato, una somma sull’intero intervallo di tempo. Non dice nulla su come l’ampiezza di ciascuna componente stagionale possa variare nel tempo nel set di dati.
Per catturare quella variazione, devi invece usare lo spettrogramma di Fourier. È come il periodogramma, ma viene eseguito ripetutamente in molte finestre temporali nell’intero set di dati. Sia il periodogramma che lo spettrogramma sono disponibili come metodi nella libreria Scipy.
Tracciamo lo spettrogramma per le componenti stagionali con periodi di 2 e 4 trimestri, menzionate sopra. Come sempre, il codice completo si trova nel taccuino associato collegato alla fine.
spectrum = compute_spectrum(df('production'), 4, 0.1)
plot_spectrogram(spectrum, figsize_x=10)
Ciò che questo diagramma mostra è l’ampiezza, la “forza” delle componenti dei 2 quarti e dei 4 quarti nel tempo. Inizialmente sono piuttosto deboli, ma diventano molto forti intorno al 2010, il che corrisponde alle variazioni che puoi vedere nel grafico del set di dati nella parte superiore di questo articolo.
Cosa accadrebbe se, invece di fornire al modello caratteristiche stagionali ad ampiezza fissa, regolassimo l’ampiezza di queste caratteristiche nel tempo, in modo che corrisponda a ciò che ci dice lo spettrogramma? Il modello finale avrebbe prestazioni migliori nella convalida?
Scegliamo la componente stagionale dei 4 trimestri. Potremmo adattare un modello lineare (chiamato modello di inviluppo) sul trend ordine=2 di questo componente, sui dati del treno (model.fit()), ed estendere tale trend alla validazione/test (model.predict()):
envelope_features = DeterministicProcess(index=X.index, constant=True, order=2).in_sample()spec4_train = compute_spectrum(df('production').loc(index_train), max_period=4)
spec4_train
spec4_model = LinearRegression()
spec4_model.fit(envelope_features.loc(spec4_train.index), spec4_train('4.0'))
spec4_regress = pd.Series(spec4_model.predict(envelope_features), index=X.index)
ax = spec4_train('4.0').plot(label='component envelope', color='gray')
spec4_regress.loc(spec4_train.index).plot(ax=ax, color='C0', label='envelope regression: past')
spec4_regress.loc(index_test).plot(ax=ax, color='C3', label='envelope regression: future')
_ = ax.legend()
La linea blu è la forza della variazione della componente di 4 quarti nei dati del treno, adattata come tendenza quadratica (ordine=2). La linea rossa è la stessa cosa, estesa (prevista) sui dati di validazione.
Abbiamo modellato la variazione nel tempo della componente stagionale dei 4 trimestri. Possiamo prendere l’output del modello di inviluppo e moltiplicarlo per le dummy temporali corrispondenti alla componente stagionale di 4 trimestri:
spec4_regress = spec4_regress / spec4_regress.mean()season_columns = ('s(1,4)', 's(2,4)', 's(3,4)', 's(4,4)')
for c in season_columns:
X(c) = X(c) * spec4_regress
print(X)
const trend trend_squared s(1,4) s(2,4) s(3,4) s(4,4)
time
1956Q1 1.0 1.0 1.0 0.179989 0.000000 0.000000 0.000000
1956Q2 1.0 2.0 4.0 0.000000 0.181109 0.000000 0.000000
1956Q3 1.0 3.0 9.0 0.000000 0.000000 0.182306 0.000000
1956Q4 1.0 4.0 16.0 0.000000 0.000000 0.000000 0.183581
1957Q1 1.0 5.0 25.0 0.184932 0.000000 0.000000 0.000000
... ... ... ... ... ... ... ...
2013Q1 1.0 229.0 52441.0 2.434701 0.000000 0.000000 0.000000
2013Q2 1.0 230.0 52900.0 0.000000 2.453436 0.000000 0.000000
2013Q3 1.0 231.0 53361.0 0.000000 0.000000 2.472249 0.000000
2013Q4 1.0 232.0 53824.0 0.000000 0.000000 0.000000 2.491139
2014Q1 1.0 233.0 54289.0 2.510106 0.000000 0.000000 0.000000(233 rows x 7 columns)
I 4 manichini temporali non sono più né 0 né 1. Sono stati moltiplicati per l’inviluppo del componente e ora la loro ampiezza varia nel tempo, proprio come l’inviluppo.
Addestriamo nuovamente il modello principale, ora utilizzando i manichini temporali modificati.
do_forecast(X, index_train, index_test, trend_order)
RMSLE: 0.02546321729737165
Non puntiamo a un adattamento perfetto qui, poiché si tratta solo di un modello giocattolo, ma è ovvio che il modello funziona meglio, poiché segue più da vicino le variazioni di 4 quarti dell’obiettivo. Anche il parametro delle prestazioni è migliorato del 51%, il che non è affatto male.
Migliorare le prestazioni del modello è un argomento vasto. Il comportamento di qualsiasi modello non dipende da una singola caratteristica o da una singola tecnica. Tuttavia, se stai cercando di estrarre tutto il possibile da un determinato modello, probabilmente dovresti fornirgli funzionalità significative. Le dummy temporali, o coppie di Fourier seno/coseno, sono più significative quando riflettono la variazione nel tempo della stagionalità che stanno modellando.
La regolazione dell’inviluppo della componente stagionale tramite la trasformata di Fourier è particolarmente efficace per i modelli lineari. Gli alberi potenziati non apportano grandi benefici, ma puoi comunque vedere miglioramenti quasi indipendentemente dal modello che usi. Se stai utilizzando un modello ibrido, in cui un modello lineare gestisce caratteristiche deterministiche (calendario, ecc.), mentre un modello ad alberi potenziati gestisce caratteristiche più complesse, è importante che il modello lineare “faccia tutto bene”, lasciando quindi meno lavoro da fare. fare per l’altro modello.
È inoltre importante che i modelli di inviluppo utilizzati per regolare le caratteristiche stagionali vengano addestrati solo sui dati del treno e non visualizzino alcun dato di test durante l’addestramento, proprio come qualsiasi altro modello. Una volta adattato l’inviluppo, le dummy temporali contengono informazioni provenienti dall’obiettivo: non sono più caratteristiche puramente deterministiche, che possono essere calcolate in anticipo su qualsiasi orizzonte previsionale arbitrario. Quindi a questo punto le informazioni potrebbero fuoriuscire dalla convalida/test nei dati di addestramento se non stai attento.
Il set di dati utilizzato in questo articolo è disponibile qui con la licenza di dominio pubblico (CC0):
Il codice utilizzato in questo articolo può essere trovato qui:
Un taccuino inviato al concorso Vendite in negozio – Previsione delle serie temporali su Kaggle, utilizzando le idee descritte in questo articolo:
Un repository GitHub contenente la versione di sviluppo del notebook inviato a Kaggle è qui:
Tutte le immagini e il codice utilizzati in questo articolo sono creati dall’autore.
Fonte: towardsdatascience.com


