Questo post del blog è disponibile come file taccuino jupyter su GitHub.
Gli ampliamenti sono diventati una componente indispensabile nel regno delle condutture di visione artificiale. Tuttavia, la loro popolarità non ha raggiunto gli stessi livelli in altri ambiti, come ad esempio le serie temporali. In questo tutorial, approfondirò il mondo degli aumenti delle serie temporali, facendo luce sul loro significato e fornendo esempi concreti della loro applicazione utilizzando la potente libreria di modellazione di serie temporali generative, TSGM (5).
Il nostro punto di partenza è un set di dati indicato (𝐗, 𝐲). Qui, 𝐱ᵢ ∈ 𝐗 sono serie temporali multivariate (ovvero, ogni punto temporale è un vettore di caratteristiche multidimensionali) e y sono etichette. La previsione delle etichette y è chiamata attività downstream. Il nostro obiettivo è utilizzare (𝐗, 𝐲) per produrre campioni aggiuntivi (𝐗*, 𝐲*), che potrebbero aiutarci a risolvere il compito a valle in modo più efficace (in termini di prestazioni predittive o robustezza). Per semplicità, in questo tutorial non lavoreremo con le etichette, ma i metodi che descriviamo qui sono semplici da generalizzare al caso con etichette e le implementazioni software che utilizziamo possono essere facilmente estese al caso supervisionato aggiungendo parametri aggiuntivi al .generate metodo (vedi esempi sotto).
Senza ulteriori indugi, consideriamo gli aumenti delle serie temporali uno per uno.
In TSGM, tutti i potenziamenti sono organizzati in modo ordinato tsgm.models.augmentationse puoi consultare la documentazione completa disponibile su Documentazione TSGM.
Ora diamo il via agli esempi di codifica installando tsgm:
pip install tsgm
Andando avanti, importiamo tsgm e carichiamo un set di dati esemplare. Un tensore X ora contiene 100 serie temporali sinusoidali di lunghezza 64, con 2 caratteristiche ciascuna. Con spostamento, frequenze e ampiezze casuali (l’ampiezza massima è 20).
# import the libraries
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import random
from tensorflow import keras
import tsgm
# and now generate the dataset
X = tsgm.utils.gen_sine_dataset(100, 64, 2, max_value=20)
Innanzitutto, come primo aumento consideriamo il jittering.
I dati delle serie temporali vengono aumentati con rumore gaussiano casuale (Wikipedia)
In tsgm, l’aumento del rumore gaussiano può essere applicato come segue:
aug_model = tsgm.models.augmentations.GaussianNoise()
samples = aug_model.generate(X=X, n_samples=10, variance=0.2)
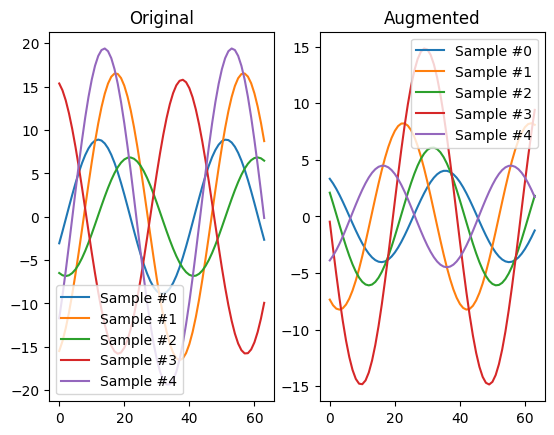
L’idea alla base dell’aumento del rumore gaussiano è che l’aggiunta di una piccola quantità di jitter alle serie temporali probabilmente non le modificherà in modo significativo ma aumenterà la quantità di campioni rumorosi nel nostro set di dati. Spesso rende i modelli a valle più robusti rispetto ai campioni rumorosi o migliora le prestazioni predittive.
Gli iperparametri del rumore gaussiano e il modo di aggiungere il rumore (ad esempio, il rumore gaussiano può aumentare verso la fine di una serie temporale) sono una questione difficile e dipendono da un particolare set di dati e da un problema a valle. Spesso vale la pena sperimentare e vedere come questi parametri influenzano le prestazioni del modello target.
Qui forniamo una visualizzazione dei campioni dal set di dati sinusoidali originali e dei campioni aumentati.
Un altro approccio all’aumento delle serie temporali è semplicemente mescolare le funzionalità. Questo approccio è adatto solo per particolari serie temporali multivariate, dove sono invarianti per tutte o particolari permutazioni di caratteristiche. Ad esempio, può essere applicato a serie temporali in cui ciascuna caratteristica rappresenta le stesse misurazioni indipendenti provenienti da vari sensori.
Per spiegare questo approccio, prendiamo l’esempio di cinque sensori identici, etichettati come S_1, S_2, S_3, S_4 e S_5. A titolo illustrativo, supponiamo che i sensori 1–4 siano probabilmente intercambiabili rispetto alle rotazioni. Quindi ha senso provare ad aumentare i dati con rotazioni di caratteristiche rispetto alle rotazioni dei sensori S_1, …, S_5.
Analogamente all’esempio precedente, l’aumento può funzionare come segue:
aug_model = tsgm.models.augmentations.Shuffle()
samples = aug_model.generate(X=X, n_samples=3)
Qui mostriamo un campione di una serie temporale con 5 funzionalità e un campione aumentato, analogamente all’immagine sopra.
L’aumento di suddivisione e riproduzione casuale (3) taglia una serie temporale in sezioni e mescola tali pezzi. Questo aumento può essere eseguito per serie temporali che presentano una qualche forma di invarianza nel tempo. Ad esempio, immagina una serie temporale misurata da dispositivi indossabili per diversi giorni. La buona strategia per questo caso è suddividere le serie temporali in giorni e, mescolando quei giorni, ottenere campioni aggiuntivi. L’aumento di sezione e riproduzione casuale è visualizzato nell’immagine seguente:
aug_model = tsgm.models.augmentations.SliceAndShuffle()
samples = aug_model.generate(X=X, n_samples=10, n_segments=3)
Consideriamo i campioni aumentati e originali:
La deformazione della grandezza (3) modifica la grandezza di ciascun campione in un set di dati di serie temporali moltiplicando la serie temporale originale con una curva spline cubica. Questo processo ridimensiona l’entità delle serie temporali, il che può essere utile in molti casi, come il nostro esempio sintetico con i seni n_knots numero di nodi a magnitudini casuali distribuiti come N(1, p^2) Dove P è impostato da un parametro sigma in funzione .generate.
aug_model = tsgm.models.augmentations.MagnitudeWarping()
samples = aug_model.generate(X=X, n_samples=10, sigma=1)
Ecco un esempio di dati originali e campioni aumentati generati con MagnitudeWarping.
In questa tecnica (4), le finestre selezionate nei dati delle serie temporali accelerano o diminuiscono. Quindi, l’intera serie temporale risultante viene ridotta alla dimensione originale per mantenere i passaggi temporali alla lunghezza originale. Vedi un esempio di tale aumento di seguito:
Tale aumento può essere utile, ad esempio, nella modellazione di apparecchiature. In tali applicazioni, le misurazioni dei sensori possono modificare la velocità del cambiamento a seconda di come vengono utilizzate tali apparecchiature.
In tsgm, come sempre, la generazione può essere effettuata tramite
aug_model = tsgm.models.augmentations.WindowWarping()
samples = aug_model.generate(X=X, n_samples=10, scales=(0.5,), window_ratio=0.5)
Di seguito è riportato un esempio di serie temporale generata.
Dynamic Time Warping Barycentric Average (DTWBA)(2) è un metodo di aumento basato sul Dynamic Time Warping (DTW). DTW è un metodo per misurare la somiglianza tra serie temporali. L’idea è di “sincronizzare” quelle serie temporali, come dimostrato nella figura seguente.
Maggiori dettagli sul calcolo DTW sono disponibili su https://rtavenar.github.io/blog/dtw.html.
DTWBA funziona così:
1. L’algoritmo seleziona una serie temporale per inizializzare il risultato DTWBA. Questa serie temporale può essere fornita esplicitamente o scelta casualmente dal set di dati
2. Per ciascuno dei N serie temporali, l’algoritmo calcola la distanza DTW e il percorso (il percorso è la mappatura che minimizza la distanza)
3. Dopo aver calcolato tutto N Distanze DTW, l’algoritmo aggiorna il risultato DTWBA facendo la media rispetto a tutti i percorsi trovati sopra
4. L’algoritmo ripete i passaggi (2) e (3) finché il risultato DTWBA converge
Un’implementazione di riferimento può essere trovata in tslearne una descrizione può essere trovata in (2).
In tsgm, i campioni possono essere generati come segue
aug_model = tsgm.models.augmentations.DTWBarycentricAveraging()
initial_timeseries = random.sample(range(X.shape(0)), 10)
initial_timeseries = X(initial_timeseries)
samples = aug_model.generate(X=X, n_samples=10, initial_timeseries=initial_timeseries )
Un altro approccio all’aumento consiste nell’addestrare un modello di apprendimento automatico su dati storici e addestrarlo a generare nuovi campioni sintetici. È un metodo blackbox perché è difficile interpretare il modo in cui sono stati generati i nuovi campioni. Nel caso delle serie temporali è possibile applicare diversi metodi; in particolare, tsgm ha processi VAE, GAN e gaussiani. Un esempio di generazione di serie temporali sintetiche con VAE è
n, n_ts, n_features = 1000, 24, 5
data = tsgm.utils.gen_sine_dataset(n, n_ts, n_features)
scaler = tsgm.utils.TSFeatureWiseScaler()
scaled_data = scaler.fit_transform(data)
architecture = tsgm.models.zoo(“vae_conv5”)(n_ts, n_features, 10)
encoder, decoder = architecture.encoder, architecture.decodervae = tsgm.models.cvae.BetaVAE(encoder, decoder)
vae.compile(optimizer=keras.optimizers.Adam())
vae.fit(scaled_data, epochs=1, batch_size=64)
samples = vae.generate(10)
Abbiamo esplorato diversi metodi per la generazione di serie temporali sintetiche. Molti di essi introducono distorsioni induttive nel modello e sono utili in contesti pratici.
Come scegliere? Innanzitutto, analizza se il tuo problema contiene invarianze. È invariante al rumore casuale? È invariante includere il mescolamento?
Successivamente, scegli un ampio insieme di metodi e verifica se qualcuno dei metodi selezionati migliora le prestazioni del tuo problema a valle (tsgm ha metrica delle prestazioni a valle). Quindi, seleziona l’insieme di metodi di aumento che offre il maggiore incremento delle prestazioni.
Ultimo, ma non meno importante, ringrazio Letizia Iannucci e Georgy Gritsenko per l’aiuto e le utili discussioni sulla stesura di questo post. Se non diversamente specificato, tutte le immagini sono dell’autore.
Questo post sul blog fa parte del progetto TSGM, in cui stiamo creando uno strumento per migliorare le pipeline di serie temporali tramite l’aumento e la generazione di dati sintetici. Se ti è stato utile, dai un’occhiata il nostro repository e valuta la possibilità di citare il documento su TSGM:
@article{
nikitin2023tsgm,
title={TSGM: A Flexible Framework for Generative Modeling of Synthetic Time Series},
author={Nikitin, Alexander and Iannucci, Letizia and Kaski, Samuel},
journal={arXiv preprint arXiv:2305.11567},
year={2023}
}
(1) H. Sakoe e S. Chiba, “Ottimizzazione dell’algoritmo di programmazione dinamica per il riconoscimento delle parole parlate”. IEEE Transactions on Acoustics, Speech, and Signal Processing, 26(1), 43–49 (1978).
(2) F. Petitjean, A. Ketterlin e P. Gancarski. Un metodo di media globale per il time warping dinamico, con applicazioni al clustering. Riconoscimento di modelli, Elsevier, 2011, vol. 44, num. 3, pp. 678–693
(3) Um TT, Pfister FM, Pichler D, Endo S, Lang M, Hirche S,
Fietzek U, Kulic´ D (2017) Aumento dei dati dei sensori indossabili per il monitoraggio della malattia di Parkinson utilizzando reti neurali convoluzionali. In: Atti della 19a conferenza internazionale ACM sull’interazione multimodale, pp. 216–220
(4) Rashid, KM e Louis, J., 2019. Window-warping: un aumento dei dati di serie temporali dei dati IMU per l’identificazione dell’attività delle macchine edili. Nell’ISARC. Atti del simposio internazionale sull’automazione e la robotica nelle costruzioni (Vol. 36, pp. 651–657). Pubblicazioni IAARC.
(5) Nikitin, A., Iannucci, L. e Kaski, S., 2023. TSGM: Un quadro flessibile per la modellazione generativa di serie temporali sintetiche. arXiv prestampa arXiv:2305.11567. Collegamento Arxiv.
Fonte: towardsdatascience.com


