A volte il trucco del kernel è inutile.
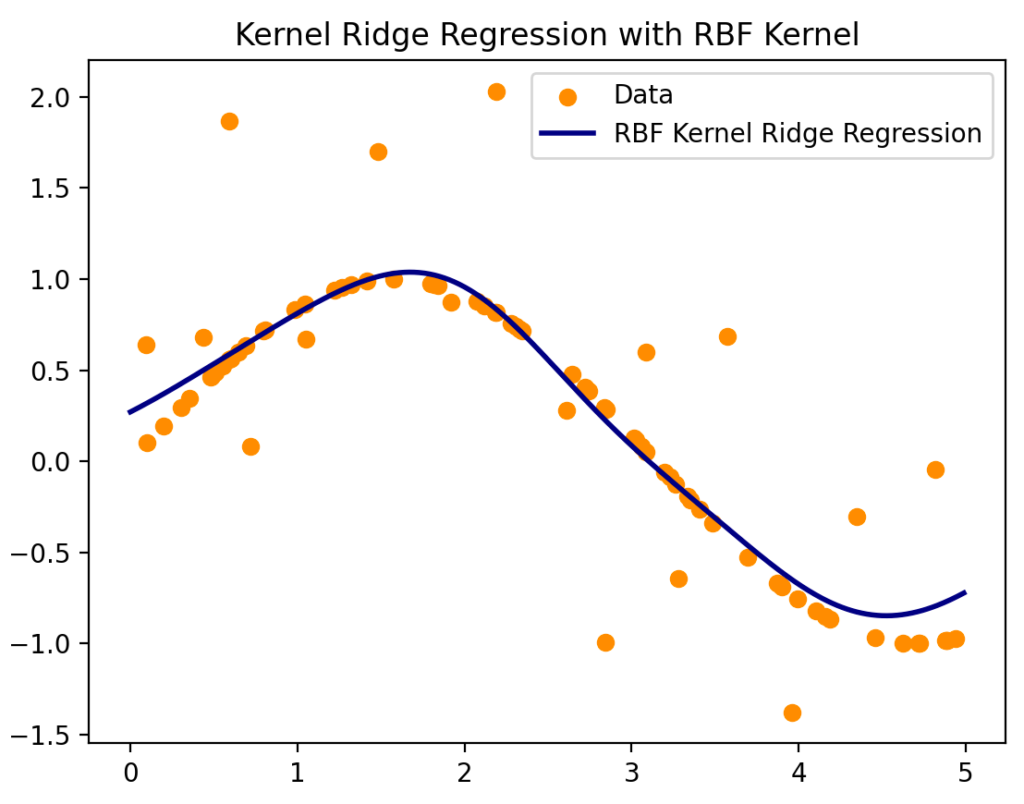
In questo post, voglio mostrare un risultato interessante che all’inizio non mi era ovvio, ovvero il seguente:
lla regressione inear e la regressione della cresta del kernel lineare senza regolarizzazione sono equivalenti.
In realtà ci sono molti concetti e tecniche coinvolti qui, quindi li esamineremo uno per uno e infine li useremo tutti per spiegare questa affermazione.
Innanzitutto, esamineremo la classica regressione lineare. Poi spiegherò cos’è il trucco del kernel e il kernel lineare, e infine mostreremo una dimostrazione matematica per l’affermazione di cui sopra.
I calcoli della regressione lineare
Il classico problema della regressione lineare dei minimi quadrati ordinari o OLS è il seguente:
Dove:
- Y è un vettore di lunghezza n ed è costituito dal valore target del modello lineare
- beta è un vettore di lunghezza m: questa è l’incognita che il modello dovrà “imparare”
- X è la matrice dei dati con forma n righe e m colonne. Diciamo spesso che abbiamo n vettori registrati nello spazio delle m-caratteristiche
Quindi l’obiettivo è trovare i valori di beta che minimizzino gli errori quadratici:
Questo problema in realtà ha una soluzione in forma chiusa ed è noto come problema dei minimi quadrati ordinari. La soluzione è:
Una volta nota la soluzione, possiamo utilizzare il modello adattato per calcolare nuovi valori Y dati nuovi valori X utilizzando:
Python per la regressione lineare
Verifichiamo i nostri calcoli con scikit-learn: ecco un codice Python che fornisce un esempio di regressione lineare, utilizzando il regressore lineare sklearn, nonché una regressione basata su numpy
Fonte: towardsdatascience.com
