L'approccio probabilistico all'autolocalizzazione in condizioni di incertezza
Sommario:
- Cos’è la localizzazione e perché un robot ne ha bisogno?
- Perché vengono utilizzati strumenti probabilistici per calcolare la localizzazione?
- Esempio end-to-end: come utilizzare gli algoritmi bayesiani per determinare la posizione di un robot in condizioni di incertezza?
Come possono le auto autonome rimanere all'interno di un'unica corsia a 60 miglia all'ora? Come può un i-robot evitare di cadere dalle scale? Come possono i robot di consegna sapere se stanno andando al cliente affamato giusto? Queste sono solo alcune delle domande a cui i veicoli autonomi devono rispondere senza l’intervento umano.
1. Cos'è la localizzazione? E perché un robot ne ha bisogno?
Come puoi immaginare, la localizzazione accurata del veicolo è fondamentale affinché il veicolo autonomo possa portare a termine i suoi compiti in modo efficace e sicuro. Il processo per stimare la posizione del veicolo dai dati dei sensori è chiamato localizzazione. La precisione della localizzazione aumenta con i sensori che aggiungono informazioni e diminuisce con il movimento del veicolo che aggiunge rumore.
2. Perché vengono utilizzati strumenti probabilistici per calcolare la localizzazione?
È possibile sfruttare gli strumenti probabilistici per migliorare la precisione della posizione laddove né i sensori né il movimento sono accurati al 100%.
Cos'è la probabilità?
Secondo la definizione del dizionario, la probabilità è una “descrizione numerica della probabilità che un evento si verifichi” (wikipedia). Tuttavia, quando si tratta del significato di probabilità, la risposta non è così semplice. Ci sono interpretazioni contrastanti della probabilità da parte di due grandi schieramenti, i frequentisti e i bayesiani.
IL Frequentista l'approccio interpreta la probabilità come la frequenza relativa nel tempo; quante volte otterrò il risultato desiderato se ripeto un esperimento molte volte?
Questo approccio è oggettivo perché chiunque esegua gli esperimenti (ad esempio lanciando una moneta) otterrà lo stesso risultato nel lungo periodo.
IL Bayesiano Questo approccio interpreta la probabilità come il grado di certezza che un evento accadrà. Quanto sono sicuro di ottenere il risultato desiderato, date le conoscenze degli esperti e i dati disponibili? Questo approccio è soggettivo, poiché rappresenta lo stato attuale delle convinzioni combinando le conoscenze precedenti (soggettive) e i dati sperimentali finora noti. Permette di stimare la probabilità di un evento singolare che non possiamo ripetere molte volte, dove il significato frequentista non si applica.
Ad esempio, se la probabilità che una data ti risponda dopo il tuo primo incontro è 0,8, allora siamo sicuri all'80% che ti sei divertito molto e la persona ti risponderà; Noi non significa che ti invieranno messaggi l'80% delle volte se ripeti il primo appuntamento ancora e ancora.
Quali sono i vantaggi della probabilità bayesiana?
La probabilità bayesiana ci consente sia di quantificare il nostro grado di convinzione sia di aggiornarlo alla luce di nuove prove.
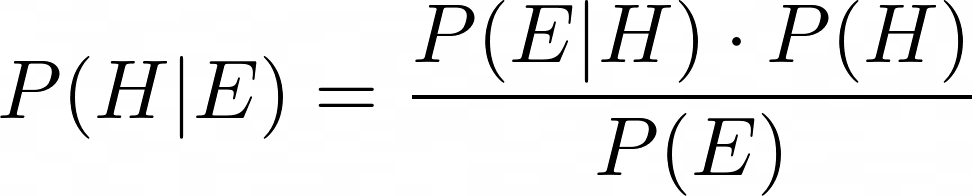
Nel nostro contesto, P(H) è la nostra ipotesi iniziale sulla posizione del robot e P(H|E) è la nostra ipotesi aggiornata dopo aver misurato l'evidenza dei sensori E.
La distribuzione di probabilità dell'ipotesi quantifica la nostra certezza nella posizione del robot.
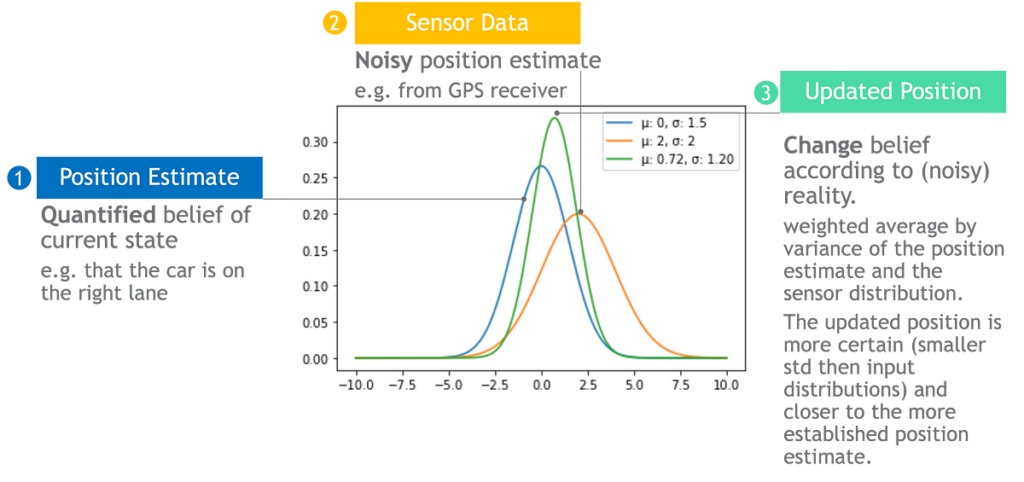
L’ipotesi può cambiare in base alle prove
Più informativi e accurati sono i dati dei sensori, maggiore sarà l’effetto che avranno. Se il sensore è perfetto, la posizione del robot si allineerà con la lettura del sensore, altrimenti se i dati del sensore sono molto rumorosi o non informativi, la posizione del robot rimarrà la stessa.
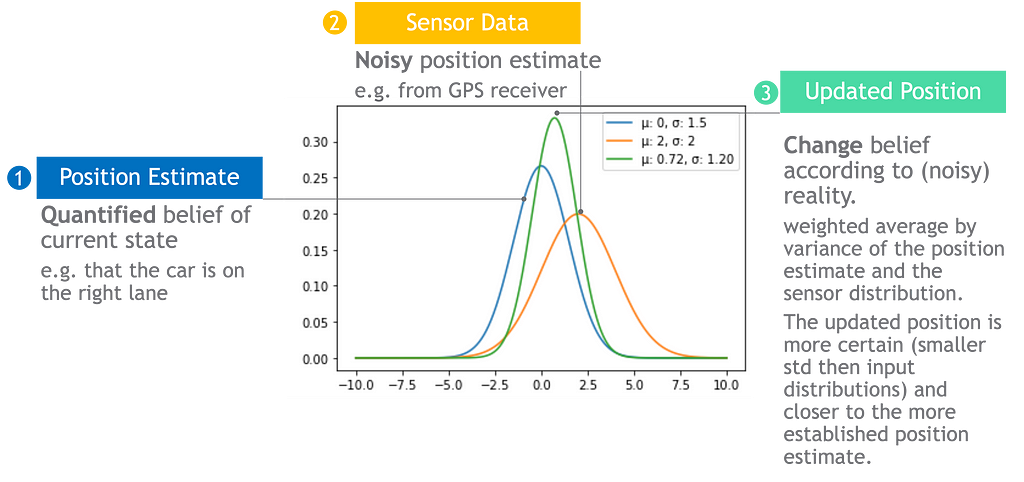
Gli aggiornamenti possono combinare più fonti di prova
Possiamo formulare la legge di Bayes per combinare più fonti di dati utilizzando la regola della catena, nota anche come regola generale del prodotto. Permette di semplificare una distribuzione congiunta di prove multiple in un prodotto di probabilità condizionate.
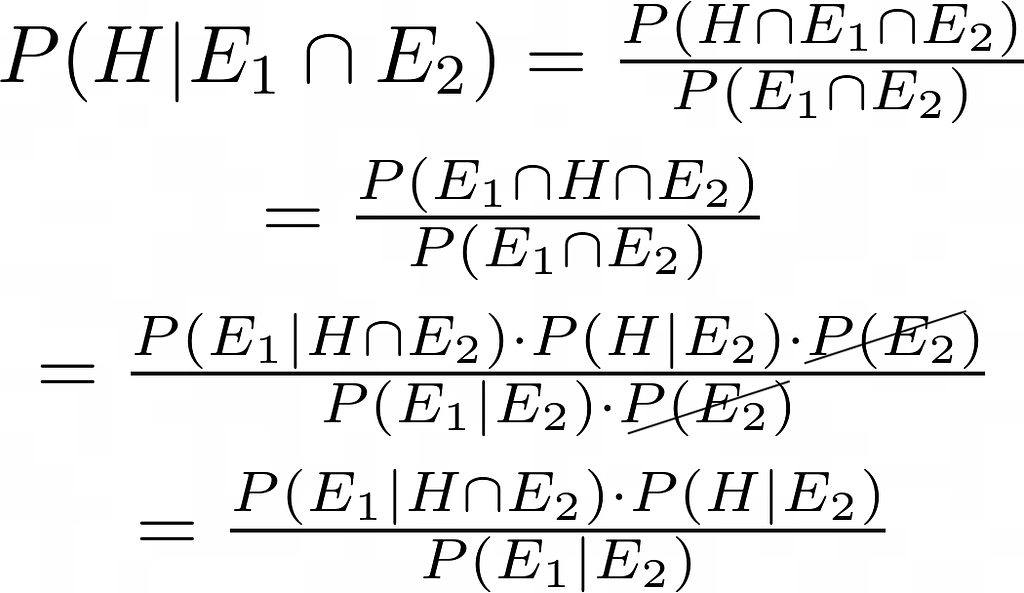
Ad esempio, utilizziamo spesso il GPS per navigare dalla nostra posizione attuale, ma il GPS funziona meglio con cielo sereno e la sua precisione è limitata a pochi metri. Le auto autonome non possono fare affidamento esclusivamente sul GPS per rimanere in una corsia larga pochi metri e per navigare nelle gallerie o nei parcheggi sotterranei. I veicoli autonomi possono compensare le carenze del GPS aggiungendo più fonti di informazione come le fotocamere.
3. Esempio end-to-end: come utilizzare gli algoritmi bayesiani per determinare la posizione del robot in condizioni di incertezza?
Esaminiamo in modo approfondito un filtro bayesiano che migliora ricorsivamente le stime della probabilità di localizzazione utilizzando l'inferenza bayesiana. La natura ricorsiva significa che l'output del filtro al tempo t_0, P(H|E), funge da input di ipotesi per il successivo timestamp t_1, P(H).
Supponiamo che un robot per le consegne stia percorrendo un percorso circolare all'interno di una stazione spaziale per trasportare rifornimenti. Il robot ha una mappa che descrive in dettaglio la conformazione del terreno e la posizione dei sensori.
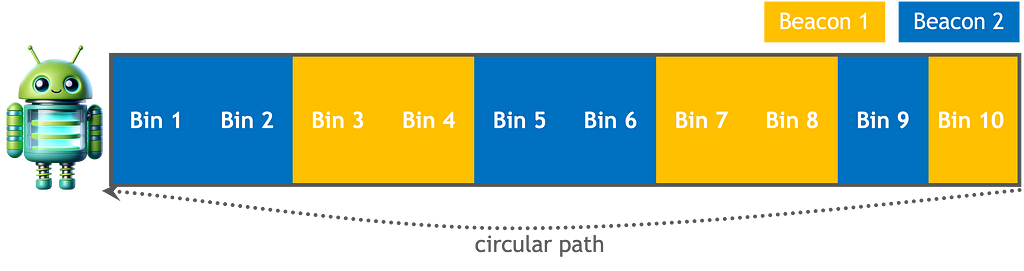
– Definizione del problema:
Ci riferiamo alla posizione stimata del robot come spazio degli stati del robot. Ad esempio, un vettore bidimensionale (ovvero una coppia ordinata di numeri) che traccia la posizione dell'asse x e la velocità dell'asse x può tracciare la posizione di un robot e modificarne la velocità in una dimensione. È possibile estendere lo spazio degli stati del robot a dimensioni aggiuntive per tracciare più dimensioni di posizione (y, z), orientamento, ecc.
Per semplicità, possiamo supporre che il nostro robot si muova a velocità costante. Il movimento aggiunge incertezza al calcolo, poiché non è affidabile al 100%. Il motore potrebbe non funzionare a una velocità specifica o il robot potrebbe incontrare ostacoli, che potrebbero causare il superamento o il mancato raggiungimento del movimento previsto da parte del robot.
Il nostro robot rileverà la sua posizione misurando la presenza di un faro. Le letture del sensore, chiamate anche spazio di misuranon sono accurati al 100%. I sensori potrebbero confondere il rumore con un segnale beacon che può portare a falsi allarmi o non riuscire affatto a rilevare un segnale.
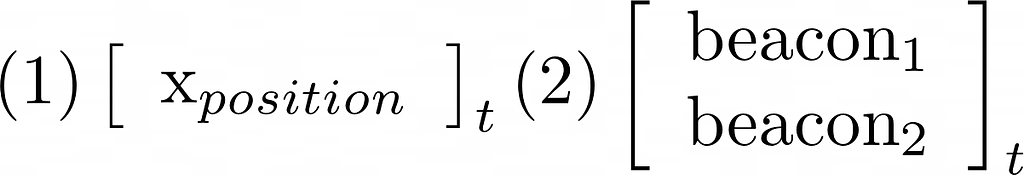
– L'algoritmo: filtro dell'istogramma
Con questo filtro bayesiano lo spazio degli stati del robot è rappresentato da un istogramma attraverso un numero finito di contenitori o regioni. È un filtro discreto, il che significa che il robot può trovarsi solo in una di queste regioni e calcoliamo la probabilità che il robot si trovi in ciascuna di queste. Inoltre, all'interno di ciascun contenitore, ad esempio un'area di 5 metri quadrati, la probabilità di trovarsi in un punto specifico è la stessa. Se vogliamo aumentare la granularità, dobbiamo aggiungere più contenitori.
Questo filtro non è parametrico, nel senso che non fa alcuna ipotesi forte sulla rappresentazione dello stato del robot e non è limitato a un tipo di distribuzione come quella gaussiana. È in grado di rappresentare stime di localizzazione complesse, come un’ipotesi multimodale che mantiene più ipotesi migliori, ma comporta un costo computazionale: una complessità esponenziale. Per aggiungere una dimensione aggiuntiva, da 1-D a 2-D mantenendo la stessa granularità, avremo bisogno di contenitori 10×10, per passare al 3-D avremo bisogno di contenitori 10x10x10 e così via. Questa è una limitazione significativa per i robot che tracciano più dimensioni e sono limitati in termini di memoria e potenza di calcolo.
– Calcolo:
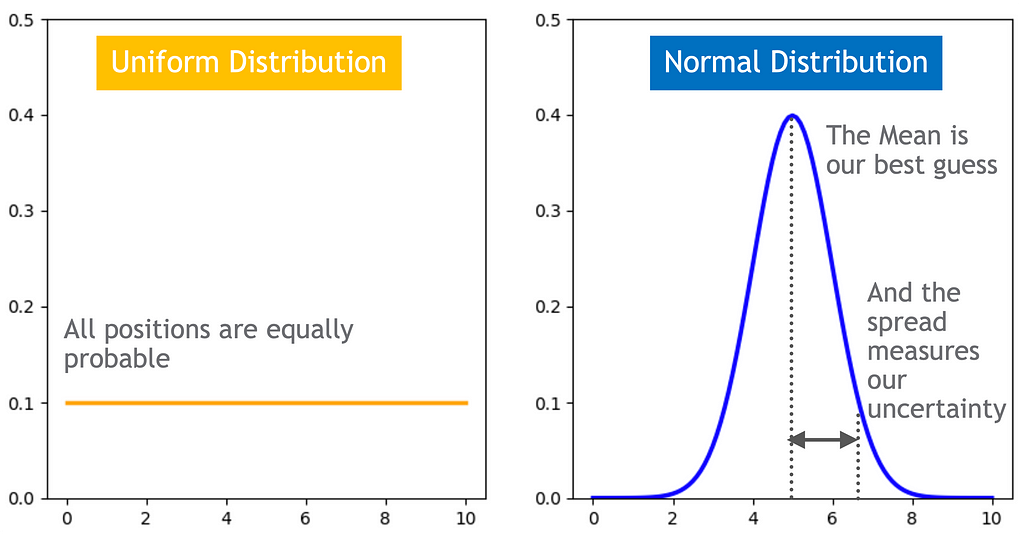
- Ipotesi iniziale: Partiamo da una località sconosciuta munita di mappa. All'inizio ogni regione è ugualmente probabile, come rappresentato da una distribuzione uniforme in tutti i contenitori.

2. Funzione di movimento: simula il movimento del robot. Il movimento del robot è stocastico, ovvero non è garantito che si sposti nel contenitore desiderato in ogni fase temporale. Per aggiornare la posizione del robot dopo ogni spostamento, calcoliamo la probabilità che il robot si trovi in ciascuna regione nella fase temporale successiva. Questo calcolo considera sia la probabilità che il robot rimanga nella stessa regione sia la probabilità che si sposti in una regione diversa.
For each movement:
For each region:
Region probability at time t+1 =
Region probability at time t x stay probability +
Probability of robot coming from the neighboring region x move probability
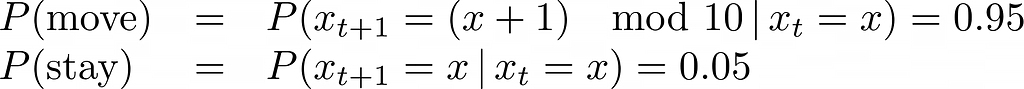
Come mostrato nell'equazione seguente, il movimento di un passo del robot non modificherà la stima della posizione a causa della distribuzione uniforme, in cui ciascuna regione ha la stessa probabilità di rimanere e muoversi.
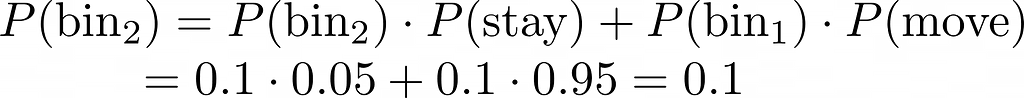
Anche se inizialmente partiamo da un contenitore con assoluta certezza (100%), la casualità intrinseca del movimento aggiungerà gradualmente rumore, portandoci verso una distribuzione uniforme nel tempo. Dobbiamo aggiungere informazioni!
3. Funzione di rilevamento: incorpora misurazioni che aggiungono informazioni utilizzando il teorema di Bayes.
After each movement:
For each region:
Region probability at time t+1 given measurement at time t+1 =
Likelihood of the measurement given the robot is in that region
x Region probability at time t+1 after movement
x normlization to ensure that all the probabilities sum to 1.
L'affidabilità dei sensori è rappresentata con probabilità, poiché non sono accurate al 100%. Le equazioni seguenti dimostrano che quando il sensore rileva il colore arancione, c'è una probabilità del 90% che il robot si trovi in un contenitore arancione e una probabilità del 10% che il sensore sia sbagliato e che il robot sia effettivamente in un contenitore blu.

Il calcolo presentato di seguito illustra che, a differenza del movimento, i sensori forniscono informazioni e migliorano la nostra comprensione della posizione del robot. Ad esempio, poiché il contenitore 2 non è arancione, la probabilità che il robot si trovi al suo interno diminuisce da 0,1 a 0,02.
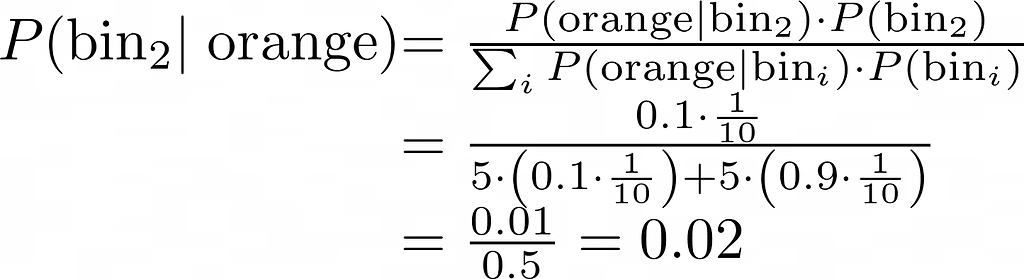
L'immagine seguente mostra l'ipotesi di posizione aggiornata dopo aver incorporato i dati di movimento e dei sensori nella nostra ipotesi iniziale.
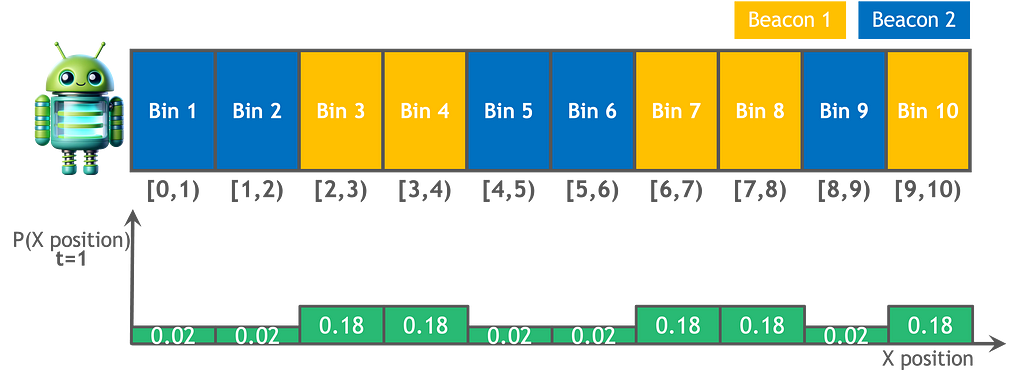
Pensieri finali
Dov'è il robot? Possiamo affinare continuamente la nostra risposta a questa domanda utilizzando filtri bayesiani ricorsivi, partendo da una distribuzione uniforme che mantiene tutte le ipotesi ugualmente probabili fino a stabilirsi su quella più probabile.
I filtri bayesiani ci aiutano a misurare la nostra fiducia nella posizione del robot, aggiornando questa convinzione integrando i dati dei sensori (rumorosi) con le informazioni precedenti (la posizione stimata del robot dopo il movimento).
Fonti:
- Questi sono i miei appunti riassuntivi delle prime lezioni del corso edX altamente raccomandato “Algoritmi bayesiani per veicoli a guida autonoma” di Dottor Roi Yozevitch.
- Robotica probabilistica GitBook: filtro non parametrico
- Wikipedia probabilità, teoria della probabilità E teorema di Bayes
- Personale di Daniel Sabinasz blog sui filtri dell'istogramma
- Convertitore online da lattice in png.
- Immagini: con cui è stato creato l'avatar del robot Dalle. Tutte le altre immagini utilizzate in questo articolo sono state create dall'autore.
Come ritrovarsi in un mondo digitale? è stato originariamente pubblicato in Verso la scienza dei dati su Medium, dove le persone continuano la conversazione evidenziando e rispondendo a questa storia.
Fonte: towardsdatascience.com


