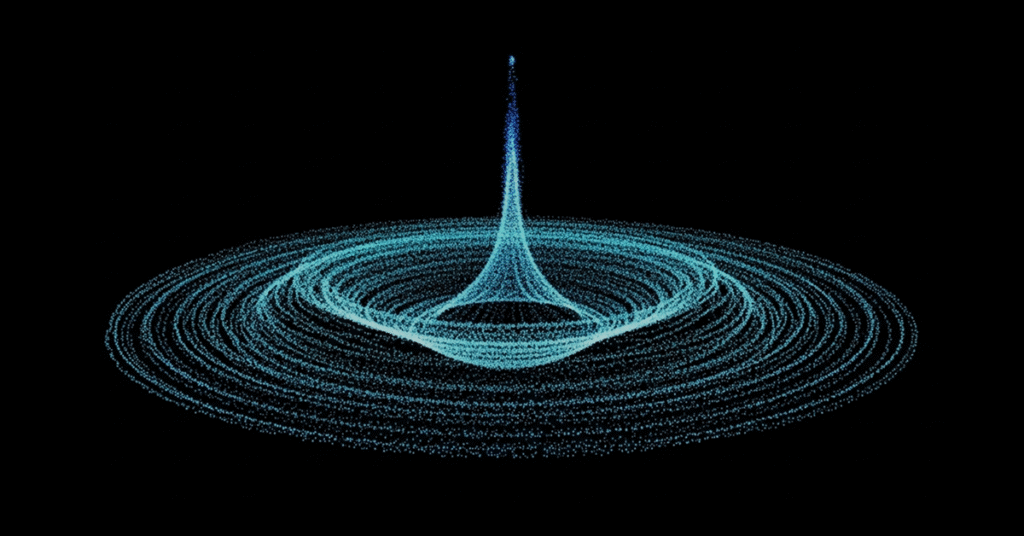
Il nostro nuovo metodo potrebbe aiutare i matematici a sfruttare le tecniche di intelligenza artificiale per affrontare sfide di lunga data in matematica, fisica e ingegneria.
Per secoli, i matematici hanno sviluppato equazioni complesse per descrivere la fisica fondamentale coinvolta nella fluidodinamica. Queste leggi regolano tutto, dal vortice vortice di un uragano a flusso d’aria che solleva l’ala di un aereo.
Gli esperti possono creare accuratamente scenari che rendono la teoria contro la pratica, portando a situazioni che non potrebbero mai accadere fisicamente. Queste situazioni, come quando quantità come la velocità o la pressione diventano infinite, sono chiamate “singolarità” o “esplosioni”. Aiutano i matematici a identificare i limiti fondamentali nelle equazioni della fluidodinamica e aiutano a migliorare la nostra comprensione di come funziona il mondo fisico.
In a Nuovo cartaIntroduciamo una famiglia completamente nuova di esplosioni matematiche ad alcune delle equazioni più complesse che descrivono il movimento fluido. Stiamo pubblicando questo lavoro in collaborazione con matematici e geofisici di istituzioni tra cui Brown University, New York University e Stanford University
Il nostro approccio presenta un nuovo modo di sfruttare le tecniche di intelligenza artificiale per affrontare le sfide di lunga data in matematica, fisica e ingegneria che richiedono precisione e interpretabilità senza precedenti.
L’importanza di singolarità instabili
La stabilità è un aspetto cruciale della formazione di singolarità. Una singolarità è considerata stabile se è robusta per piccoli cambiamenti. Al contrario, una singolarità instabile richiede condizioni estremamente precise.
Si prevede che le singolarità instabili svolgano un ruolo importante nelle domande fondamentali nella fluidodinamica perché i matematici credono che non esistano singolarità stabili per il complesso 3D senza confini Eulero E Navier-Stokes equazioni. Trovare qualsiasi singolarità nelle equazioni di Navier-Stokes è uno dei sei famosi Problemi del premio Millennium che sono ancora irrisolti.
Con i nostri nuovi metodi AI, abbiamo presentato la prima scoperta sistematica di nuove famiglie di singolarità instabili in tre diverse equazioni fluide. Abbiamo anche osservato un modello emergente quando le soluzioni diventano sempre più instabili. Il numero che caratterizza la velocità di Blow Up, lambda (λ), può essere tracciato contro l’ordine di instabilità, che è il numero di modi unici in cui la soluzione può deviare dal colpo. Il modello era visibile in due delle equazioni studiate, i media porosi incomprimibili (IPM) e le equazioni Boussinesq. Ciò suggerisce l’esistenza di soluzioni più instabili, i cui ipotesi valori di lambda si trovano lungo la stessa linea.
Abbiamo scoperto questi singolari incorporando tecniche di apprendimento automatico come ottimizzatori di secondo ordine per la formazione di reti neurali. Questi metodi ci hanno permesso di perfezionare la nostra precisione a un livello senza precedenti. Per riferimento, i nostri più grandi errori affrontati sono equivalenti a prevedere il diametro della Terra a pochi centimetri.
Qui mostriamo un esempio del campo di vorticità (ω) trovato per una delle equazioni studiate. Questa è una misura di quanto il fluido gira in ogni punto.
Mostriamo anche una fetta unidimensionale attraverso lo stesso campo lungo un asse per tutte le instabilità che abbiamo scoperto, mostrando l’evoluzione di singolarità sempre più instabili.
Metodo nuovo naviga un vasto paesaggio di singolarità
Il nostro approccio si basa sull’uso di reti neurali informate sulla fisica (PINNS). A differenza delle reti neurali convenzionali che apprendono da vasti set di dati, abbiamo addestrato i nostri modelli per abbinare le equazioni che modellano le leggi della fisica. L’output della rete è costantemente verificato rispetto a ciò che le equazioni fisiche si aspettano e apprende minimizzando il suo “residuo”, l’importo in base alla quale la sua soluzione non riesce a soddisfare le equazioni.
Il nostro uso dei pinn va oltre il loro ruolo tipico di strumenti per scopi generali utilizzati per risolvere equazioni differenziali parziali (PDE). Incorporando intuizioni matematiche direttamente nella formazione, siamo stati in grado di catturare soluzioni sfuggenti-come singolarità instabili-che hanno metodi convenzionali a lungo errati.
Allo stesso tempo, abbiamo sviluppato un framework ad alta precisione che spinge i pinn alla precisione della quasi macchina, consentendo il livello di accuratezza richiesto per rigorose prove assistite da computer.
Una nuova era di matematica assistita da computer
Questa svolta rappresenta un nuovo modo di fare ricerche matematiche, combinando approfondimenti matematici con AI all’avanguardia. Siamo entusiasti di questo lavoro per aiutare a inaugurare una nuova era in cui le sfide di lunga data vengono affrontate con AI e prove assistite da computer.
Fonte: deepmind.google


