Le Generative Adversarial Network (GAN) sono diventate estremamente popolari per la loro capacità di generare immagini belle e realistiche e modelli linguistici (ad esempio ChatGPT) che sono sempre più utilizzati in ogni settore. Questi modelli GAN sono probabilmente la ragione per cui l’intelligenza artificiale e l’apprendimento automatico hanno suscitato l’entusiasmo (o la paura) che il mondo riserva a questo settore in questo momento; perché ha mostrato a tutti (soprattutto a chi non è del settore) l’immenso potenziale che racchiude il machine learning. Esistono già molte risorse online sui modelli GAN, ma la maggior parte di queste si concentra sulla generazione di immagini. Questi modelli di generazione di immagini e linguaggio richiedono complesse complessità spaziali o temporali che aggiungono ulteriori complessità che rendono più difficile per i lettori comprendere la vera essenza dei GAN.
Nel tentativo di porre rimedio a questo problema e rendere i GAN più accessibili a un pubblico più ampio, in questa breve discussione e nell’esempio del modello GAN, adotteremo un approccio diverso e più pratico incentrato sulla generazione di dati sintetici di funzioni matematiche. Oltre ad essere una semplificazione a fini di apprendimento, la generazione di dati sintetici sta diventando sempre più importante di per sé. I dati non solo svolgono un ruolo centrale nel processo decisionale aziendale, ma vi è anche un numero crescente di usi in cui un approccio basato sui dati sta diventando più popolare rispetto ai modelli a principio primo. Un esempio interessante di ciò sono le previsioni del tempo, il primo modello di principio includeva versioni semplificate dell’equazione di Navier-Stokes che veniva risolta numericamente (con costi computazionali significativi, dovrei aggiungere). Tuttavia, i recenti tentativi di previsioni meteorologiche con il deep learning (ad esempio, guarda FourCastNet di Nvidia (1)) hanno avuto molto successo nell’acquisizione dei modelli meteorologici e, una volta addestrati, è più facile e molto più veloce da eseguire.
Modelli generativi e modelli discriminativi
Nell’apprendimento automatico, è importante comprendere la distinzione tra modelli discriminativi e generativi poiché sono i componenti chiave di un GAN. Sveliamo questi termini (molto brevemente):
Modelli discriminativi:
I modelli discriminativi si concentrano sulla classificazione dei dati in classi predefinite, ad esempio classificando immagini di cani e gatti nelle rispettive classi. Invece di catturare l’intera distribuzione, questi modelli individuano i confini che separano le diverse classi. Danno come risultato P(y|x) (probabilità della classe, y dati i dati di input, x), cioè rispondono alla domanda a quale categoria appartiene un dato punto dati?
Modelli generativi:
I modelli generativi mirano a comprendere la struttura sottostante dei dati. A differenza dei modelli discriminativi che distinguono tra classi, i modelli generativi apprendono l’intera distribuzione dei dati. Questi modelli restituiscono p(x|y), ovvero rispondono alla domanda: qual è la probabilità di generare questo punto dati specifico data la classe specificata?
L’interazione tra questi due modelli costituisce il fondamento stesso dei GAN.
GAN: struttura e componenti
Esploriamo ora come questi concetti si uniscono in un modello GAN. I componenti chiave di un GAN includono il vettore del rumore, il generatore e il discriminatore.
Il generatore: generazione di dati realistici
Per generare dati sintetici il generatore utilizza un vettore di rumore casuale come input. Nel tentativo di ingannare il discriminatore, il generatore mira ad apprendere la distribuzione dei dati reali e produrre dati sintetici che non possono essere distinti dai dati reali. Un problema qui è che per lo stesso input produrrebbe sempre lo stesso output (immagina un generatore di immagini che produca un’immagine realistica ma sempre la stessa immagine, che non è molto utile). Il vettore di rumore casuale introduce casualità nel processo, fornendo diversità nell’output generato.
Il discriminatore: discernere il vero dal falso
Il discriminatore è come un critico d’arte addestrato a distinguere tra dati reali e falsi. Il suo ruolo è quello di esaminare attentamente i dati che riceve e assegnare un punteggio di probabilità che l’opera sia reale. Se i dati sintetici sembrano simili ai dati reali, il discriminatore assegna un punteggio di probabilità alto, altrimenti assegna un punteggio di probabilità basso.
Addestramento contraddittorio: un duello dinamico
Il generatore si sforza di imparare a produrre dati sintetici che il discriminatore non può differenziare dai dati reali. Allo stesso tempo, il discriminatore impara e migliora anche la sua capacità di differenziare il reale dal sintetico. Questo processo formativo dinamico spinge entrambi i modelli ad affinare le proprie competenze. I due modelli sono sempre in competizione tra loro (da qui il nome “Adversarial”) e attraverso questa competizione entrambi i modelli diventano eccellenti nei loro ruoli.
Implementazione di un GAN con Pytorch
Andiamo avanti guardando un esempio di creazione di un GAN. In questo esempio, implementiamo un modello in pytorch in grado di generare dati sintetici. Per l’addestramento, abbiamo un set di dati di 6 parametri con le seguenti forme (tutti i parametri sono tracciati in funzione del parametro 1). Ogni parametro è stato scelto deliberatamente con una distribuzione e una forma significativamente diverse per aumentare la complessità del set di dati e imitare i dati del mondo reale. Tuttavia, vale la pena ricordare che esiste un margine significativo per ottimizzare sia l’architettura del discriminatore che quella del generatore, ma non ci concentreremo in questo tutorial.
In questo tutorial, presumo che tu abbia già una comprensione delle normali architetture del modello ANN e di Python. Ho fornito commenti nel codice per aiutarti a seguire il codice.
Definizione delle componenti del modello GAN (Generatore e Discriminatore)
import torch
from torch import nn
from tqdm.auto import tqdm
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt
import torch.nn.init as init
import pandas as pd
import numpy as np
from torch.utils.data import Dataset# defining a single generation block function
def FC_Layer_blockGen(input_dim, output_dim):
single_block = nn.Sequential(
nn.Linear(input_dim, output_dim),
nn.ReLU()
)
return single_block
# DEFINING THE GENERATOR
class Generator(nn.Module):
def __init__(self, latent_dim, output_dim):
super(Generator, self).__init__()
self.model = nn.Sequential(
nn.Linear(latent_dim, 256),
nn.ReLU(),
nn.Linear(256, 512),
nn.ReLU(),
nn.Linear(512, 512),
nn.ReLU(),
nn.Linear(512, output_dim),
nn.Tanh()
)
def forward(self, x):
return self.model(x)
#defining a single discriminattor block
def FC_Layer_BlockDisc(input_dim, output_dim):
return nn.Sequential(
nn.Linear(input_dim, output_dim),
nn.ReLU(),
nn.Dropout(0.4)
)
# Defining the discriminator
class Discriminator(nn.Module):
def __init__(self, input_dim):
super(Discriminator, self).__init__()
self.model = nn.Sequential(
nn.Linear(input_dim, 512),
nn.ReLU(),
nn.Dropout(0.4),
nn.Linear(512, 512),
nn.ReLU(),
nn.Dropout(0.4),
nn.Linear(512, 256),
nn.ReLU(),
nn.Dropout(0.4),
nn.Linear(256, 1),
nn.Sigmoid()
)
def forward(self, x):
return self.model(x)
#Defining training parameters
batch_size = 128
num_epochs = 500
lr = 0.0002
num_features = 6
latent_dim = 20
# MODEL INITIALIZATION
generator = Generator(noise_dim, num_features)
discriminator = Discriminator(num_features)
# LOSS FUNCTION AND OPTIMIZERS
criterion = nn.BCELoss()
gen_optimizer = torch.optim.Adam(generator.parameters(), lr=lr)
disc_optimizer = torch.optim.Adam(discriminator.parameters(), lr=lr)
Inizializzazione del modello ed elaborazione dei dati
# IMPORTING DATA
file_path = 'SamplingData7.xlsx'
data = pd.read_excel(file_path)
X = data.values
X_normalized = torch.FloatTensor((X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0)) * 2 - 1)
real_data = X_normalized#Creating a dataset
class MyDataset(Dataset):
def __init__(self, dataframe):
self.data = dataframe.values.astype(float)
self.labels = dataframe.values.astype(float)
def __len__(self):
return len(self.data)
def __getitem__(self, idx):
sample = {
'input': torch.tensor(self.data(idx)),
'label': torch.tensor(self.labels(idx))
}
return sample
# Create an instance of the dataset
dataset = MyDataset(data)
# Create DataLoader
dataloader = DataLoader(dataset, batch_size=batch_size, shuffle=True, drop_last=True)
def weights_init(m):
if isinstance(m, nn.Linear):
init.xavier_uniform_(m.weight)
if m.bias is not None:
init.constant_(m.bias, 0)
pretrained = False
if pretrained:
pre_dict = torch.load('pretrained_model.pth')
generator.load_state_dict(pre_dict('generator'))
discriminator.load_state_dict(pre_dict('discriminator'))
else:
# Apply weight initialization
generator = generator.apply(weights_init)
discriminator = discriminator.apply(weights_init)
Formazione del modello
model_save_freq = 100latent_dim =20
for epoch in range(num_epochs):
for batch in dataloader:
real_data_batch = batch('input')
# Train discriminator on real data
real_labels = torch.FloatTensor(np.random.uniform(0.9, 1.0, (batch_size, 1)))
disc_optimizer.zero_grad()
output_real = discriminator(real_data_batch)
loss_real = criterion(output_real, real_labels)
loss_real.backward()
# Train discriminator on generated data
fake_labels = torch.FloatTensor(np.random.uniform(0, 0.1, (batch_size, 1)))
noise = torch.FloatTensor(np.random.normal(0, 1, (batch_size, latent_dim)))
generated_data = generator(noise)
output_fake = discriminator(generated_data.detach())
loss_fake = criterion(output_fake, fake_labels)
loss_fake.backward()
disc_optimizer.step()
# Train generator
valid_labels = torch.FloatTensor(np.random.uniform(0.9, 1.0, (batch_size, 1)))
gen_optimizer.zero_grad()
output_g = discriminator(generated_data)
loss_g = criterion(output_g, valid_labels)
loss_g.backward()
gen_optimizer.step()
# Print progress
print(f"Epoch {epoch}, D Loss Real: {loss_real.item()}, D Loss Fake: {loss_fake.item()}, G Loss: {loss_g.item()}")
Valutazione e visualizzazione dei risultati
import seaborn as sns# Generate synthetic data
synthetic_data = generator(torch.FloatTensor(np.random.normal(0, 1, (real_data.shape(0), noise_dim))))
# Plot the results
fig, axs = plt.subplots(2, 3, figsize=(12, 8))
fig.suptitle('Real and Synthetic Data Distributions', fontsize=16)
for i in range(2):
for j in range(3):
sns.histplot(synthetic_data(:, i * 3 + j).detach().numpy(), bins=50, alpha=0.5, label='Synthetic Data', ax=axs(i, j), color='blue')
sns.histplot(real_data(:, i * 3 + j).numpy(), bins=50, alpha=0.5, label='Real Data', ax=axs(i, j), color='orange')
axs(i, j).set_title(f'Parameter {i * 3 + j + 1}', fontsize=12)
axs(i, j).set_xlabel('Value')
axs(i, j).set_ylabel('Frequency')
axs(i, j).legend()
plt.tight_layout(rect=(0, 0.03, 1, 0.95))
plt.show()
# Create a 2x3 grid of subplots
fig, axs = plt.subplots(2, 3, figsize=(15, 10))
fig.suptitle('Comparison of Real and Synthetic Data', fontsize=16)
# Define parameter names
param_names = ('Parameter 1', 'Parameter 2', 'Parameter 3', 'Parameter 4', 'Parameter 5', 'Parameter 6')
# Scatter plots for each parameter
for i in range(2):
for j in range(3):
param_index = i * 3 + j
sns.scatterplot(real_data(:, 0).numpy(), real_data(:, param_index).numpy(), label='Real Data', alpha=0.5, ax=axs(i, j))
sns.scatterplot(synthetic_data(:, 0).detach().numpy(), synthetic_data(:, param_index).detach().numpy(), label='Generated Data', alpha=0.5, ax=axs(i, j))
axs(i, j).set_title(param_names(param_index), fontsize=12)
axs(i, j).set_xlabel(f'Real Data - {param_names(param_index)}')
axs(i, j).set_ylabel(f'Real Data - {param_names(param_index)}')
axs(i, j).legend()
plt.tight_layout(rect=(0, 0.03, 1, 0.95))
plt.show()
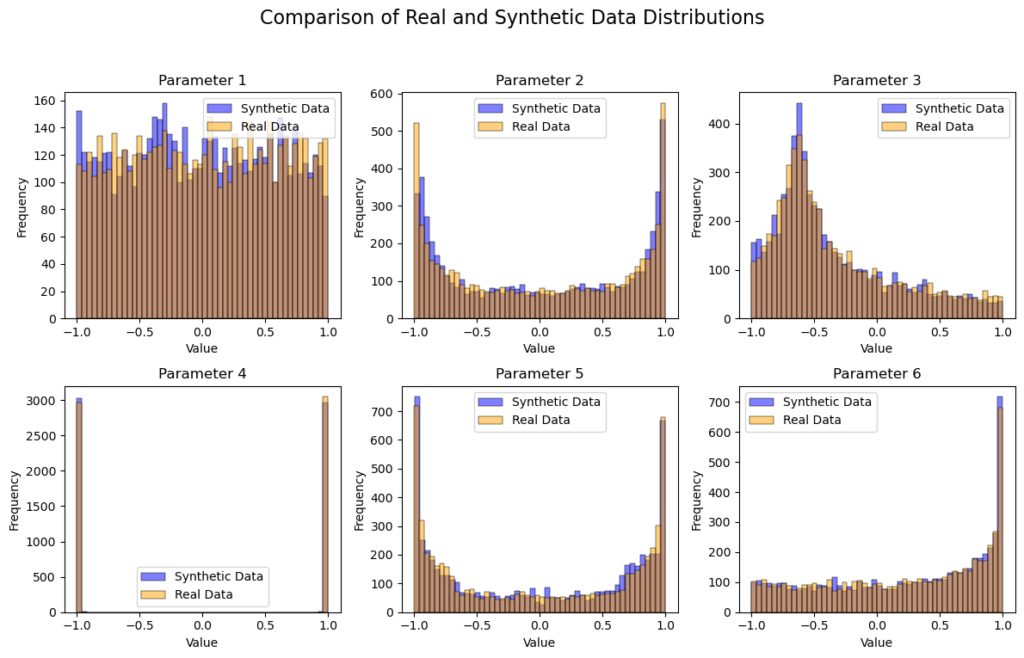
Nonostante la semplicità del nostro modello, la distribuzione e la forma matematica dei dati sintetici e dei dati reali sembrano molto simili! Il processo di addestramento e l’architettura del modello potrebbero essere modificati per una maggiore precisione, qualcosa su cui non ci siamo concentrati qui. Questo modello potrebbe essere facilmente adattato per produrre dati sintetici per altre applicazioni con parametri numerici maggiori e maggiore complessità per sistemi fisici reali. Grazie per aver dedicato del tempo a leggere, spero che tu abbia trovato questa lettura istruttiva. Ci sono così tante cose che si possono fare con i GAN, è un argomento molto interessante al momento, gioca sicuramente con questo codice per avere un’idea generale dei GAN e poi iniziare a sperimentare altre idee! buona fortuna!
Se non diversamente specificato, tutte le immagini sono dell’autore
Riferimenti
(1) Jaideep Pathak, Shashank Subramanian, Peter Harrington, Sanjeev Raja, Ashesh Chattopadhyay, Morteza Mardani, Thorsten Kurth, David Hall, Zongyi Li, Kamyar Azizzadenesheli, Pedram Hassanzadeh, Karthik Kashinath, Animashree Anandkumar. (2022). FourCastNet: un modello meteorologico globale ad alta risoluzione basato su dati che utilizza operatori neurali adattivi di Fourier. arXiv:2202.11214. https://doi.org/10.48550/arXiv.2202.11214
(2) Ghosheh, Ghadeer e Jin, Li e Zhu, Tingting. (2023). Un’indagine sulle reti avversarie generative per la sintesi di cartelle cliniche elettroniche strutturate. Sondaggi informatici ACM. 10.1145/3636424.
Fonte: towardsdatascience.com


