Prefazione
Questa è la prima aggiunta a quella che diventerà una serie continuativa sulle basi dell’algebra lineare, la matematica fondamentale dietro l’apprendimento automatico. Questo articolo sarebbe più utile ai lettori se letto insieme a Algebra lineare e le sue applicazioni di David C. Lay, Steven R. Lay e Judi J. McDonald. Considera questa serie come una risorsa complementare esterna.
Attraverso questi saggi, spero di consolidare la mia comprensione di questi concetti fondamentali e, se possibile, di offrire ulteriore chiarezza agli altri con quello che spero sia un approccio intuitivo all’apprendimento della matematica. Se ci sono errori o opportunità per me di elaborare ulteriormente, per favore condividilo e potrò apportare le modifiche necessarie.
Sfondo
Le equazioni lineari e i sistemi di equazioni lineari hanno una varietà di applicazioni nel mondo reale nei settori della finanza, ingegneria, chimica, informatica, statistica e fisica e oltre. In Chimica, le equazioni lineari vengono utilizzate per bilanciare le reazioni chimiche e calcolare le quantità di reagenti e prodotti. Questa pietra angolare dell’algebra lineare appare anche in fisica, dove le equazioni lineari vengono utilizzate all’interno della cinematica e della termodinamica per descrivere il movimento degli oggetti, aiutando a calcolare distanze, velocità e accelerazioni e a modellare rispettivamente il trasferimento di calore e il flusso di energia nei sistemi fisici. Il campo finanziario si basa su equazioni e sistemi lineari per il budget e l’analisi del portafoglio, mentre gli ingegneri potrebbero utilizzare gli stessi strumenti per condurre analisi strutturali per modellare forze e sollecitazioni negli edifici. L’algebra lineare è onnipresente; tutti possono apprezzarlo in una certa misura.
Equazioni lineari
UN equazione lineare è un’equazione con una o più variabili e per ciascuna variabile, l’esponente a cui viene elevata la variabile deve essere uno. Può essere scritto nella forma: a₁x₁ + a₂x₂ +…+ 2ᵣxᵣ = B. I valori (a₁, a₁…, andᵣ) E B sono indicati come coefficienti di un’equazione lineare.
Esempi di equazioni lineari includono: 2X +5sì = 10, 6X = 18,7v +8w +0X +2sì +3z = 15 e 3x₁ + 4x₂ + 5x₃+9x₄ + 10x₇ = 3.
Un non esempio di equazione lineare sarebbe 2x² +6X +5 = 2; questa è un’istanza di un’equazione quadratica*. Un altro non-esempio potrebbe essere 7x₁ +3x₂ = x₁* sì₁; la ragione di ciò diventa evidente quando si rappresenta graficamente questa equazione, può essere riorganizzata per formare la funzione razionale sì = 7X / X – 3 che è curvo anziché lineare.
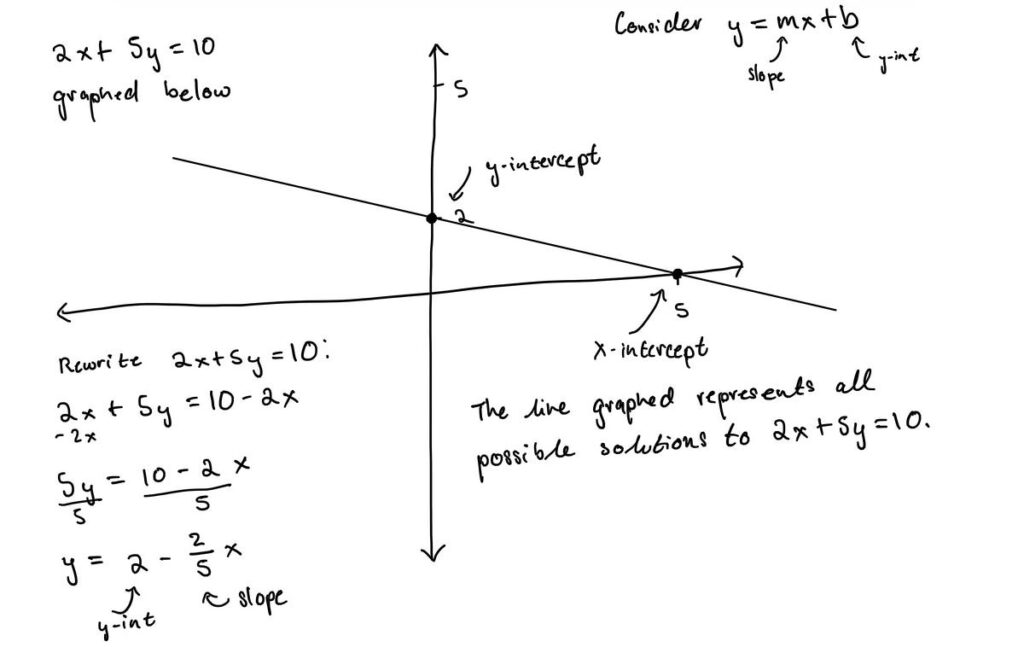
Considera l’equazione lineare 2X +5sì = 10. Il diagramma seguente illustra la rappresentazione grafica dell’equazione lineare, noterai che è una linea. Ciò diventa più evidente quando si ricorda l’equazione di una retta: sì = mx + BDove M = pendenza e B = sì intercettare. L’equazione lineare può essere riorganizzata come dimostrato di seguito per assumere questa forma.
Si può trarre la seguente conclusione: tutti (x, y) i punti che cadono sulla retta sono quindi soluzioni dell’equazione 2X +5sì = 10. Ad esempio, supponiamo di selezionare il punto di X-intercetta (5, 0) e sostituisci il X E sì valori nelle rispettive posizioni nell’equazione. 2(5) + 5(0) = 10. Qualsiasi (x, y) punto sulla linea può essere sostituito nell’equazione e l’uguaglianza rimarrà vera. Possiamo generalizzare questo risultato in una regola:
L’insieme delle soluzioni in ℝ²* per un’equazione lineare a due variabili, ax + by = c, può essere rappresentato come una linea.
Si noti che questa equazione singolare ha un numero infinito di soluzioni che si estendono su ℝ²; daremo un’occhiata più da vicino al numero di soluzioni più tardi.
Questo stesso concetto di base si trasferisce a spazi di coordinate dimensionali superiori indicati come ℝⁿ come ℝ³ in cui la linea diventa un piano a causa dell’aggiunta di una terza variabile.
Sistemi di equazioni lineari
UN sistema di equazioni lineari è una raccolta di una o più equazioni lineari con le equazioni che condividono variabili simili. Un esempio:
6X +2sì = 4
2X +4sì = 8
UN soluzione a un sistema di equazioni lineari è definito come i valori (s₁, s₂, …, sᵣ) che rendono vera ogni equazione quando sostituiscono le rispettive variabili. Nel caso del sistema sopra, la soluzione sarebbe (0, 2) perché quando (0, 2) viene sostituito nel sistema, entrambe le equazioni risultano vere.
Soluzioni di un sistema lineare
Quali sono le implicazioni grafiche di una soluzione di un sistema lineare? Quali sono i vari casi di numero di soluzioni di un sistema lineare? In questa sezione esamineremo ciascuna delle tre possibilità in maggiore dettaglio. Sono i seguenti:
- Soluzione unica
- Nessuna soluzione
- Soluzioni infinite
Soluzione unica: Nel caso di un sistema lineare a due variabili come quello sopra, la soluzione è un punto di intersezione. Perché? La soluzione è la coppia ordinata in cui entrambe le equazioni devono essere soddisfatte, se non esiste una tale coppia ordinata, ciò deve significare che le linee non si intersecano mai. Questo è un esempio di una soluzione unica. Esiste una sola soluzione che soddisfa tutte le equazioni del sistema lineare.
Nessuna soluzione: Consideriamo il caso senza soluzione. Cosa potrebbe implicare nel contesto di un sistema lineare con due variabili? In quali scenari un insieme di linee non si incontrerebbe mai? Un caso sarebbe se fossero paralleli. Nel caso di un sistema lineare in cui le rette sono tutte parallele, il sistema lineare non avrà soluzioni. Un altro caso potrebbe essere se, sebbene alcune linee possano intersecarsi con altre, non esiste un punto di intersezione comune condiviso da tutte le linee.
Soluzioni infinite: Il caso finale per un sistema lineare è l’esistenza di infinite soluzioni. Quando sarà possibile che esistano infinite soluzioni per un sistema lineare a due variabili? Se le rette sono uguali, allora ci sono infiniti punti di intersezione perché si sovrappongono, e quindi esistono infinite soluzioni. Consideriamo il seguente sistema lineare:
6X +3sì = 18
2X + sì = 6
Sebbene i coefficienti possano essere diversi, queste linee sono in realtà identiche! Se dividi ciascuno dei coefficienti della prima equazione per 3, l’equazione risultante sarà 2X + sì = 6.
La visualizzazione del numero di soluzioni per un sistema lineare cambia all’aumentare del numero di variabili. Di seguito sono raffigurati i possibili diagrammi di tutti e tre i casi di soluzione per un sistema lineare con tre variabili. Qualunque cosa dopo le tre dimensioni diventa difficile da visualizzare per il cervello umano, ma si applicano le stesse regole! Indipendentemente da quante variabili esistono, tutti i sistemi lineari non hanno soluzioni, hanno una soluzione o infinite soluzioni.
Notazione matriciale
Man mano che le equazioni lineari diventano più complesse, la notazione potrebbe diventare ingombrante. È importante che le informazioni di un sistema lineare siano condensate per essere facili da manipolare e con cui lavorare, quindi la notazione matriciale viene spesso utilizzata a favore di un insieme di equazioni. UN matrice dei coefficienti È un tipo di matrice che esclude il B coefficiente di ciascuna equazione. UN matrice aumentata è comprensivo di B coefficiente, quindi ha una colonna in più rispetto a una matrice di coefficienti.
La dimensione, denominata anche ordinedi una matrice ci dice quante righe e colonne ha una matrice. UN mxn matrice è una matrice con M righe e N colonne. Il numero di righe corrisponde a quante equazioni lineari ha un sistema mentre il numero di colonne ci dice quante variabili ci sono. Fare attenzione a garantire che il numero di righe preceda il numero di colonne poiché l’ordine non è intercambiabile.
Risoluzione di un sistema lineare
Esiste un modo sistematico per determinare se un sistema lineare ha una soluzione e, in caso affermativo, se ha una soluzione unica o infinite soluzioni, e da lì ottenere le soluzioni. La risoluzione di un sistema lineare può essere eseguita utilizzando equazioni lineari nella loro forma originale o con una matrice, sebbene sia consigliabile utilizzare una matrice poiché la notazione è più pulita e compatta. È comunque bene conoscere bene entrambi i metodi perché forniscono ulteriori informazioni sui meccanismi dell’altro.
Di seguito è riportato un processo passo passo per risolvere un sistema di equazioni senza matrice. L’idea di base è quella di creare nuove equazioni moltiplicando quelle preesistenti per ottenere equazioni identiche che possono poi essere aggiunte o sottratte da un’altra equazione per eliminare una variabile. Questo processo viene quindi ripetuto finché non abbiamo eliminato abbastanza incognite dal sistema per poter risolvere una variabile e poi risalire per risolvere il resto attraverso la sostituzione all’indietro. Alla fine è necessario verificare che la soluzione soddisfi effettivamente il sistema di equazioni.
Operazioni su righe
I passaggi delineati in precedenza sono trasferibili alla procedura centrata sulla matrice per risolvere un sistema lineare. Prendere nota di come le variabili eliminate vengono designate all’interno della matrice dopo ogni trasformazione. Prima di approfondire l’argomento, tuttavia, definiamo alcune operazioni sulle righe. Due sono in realtà parallele alle operazioni che abbiamo applicato in precedenza.
- Sostituzione: “sostituisci una riga con la somma di se stessa e di un’altra riga.”*
- Scambio: “scambia due righe.”*
- Ridimensionamento: “moltiplica tutte le voci di una riga per una costante diversa da zero.”*
Riavviciamoci ancora una volta allo stesso sistema lineare, ma questa volta utilizzando matrici e applicando operazioni sulle righe.
Nota come ho utilizzato esattamente le stesse operazioni e gli stessi fattori di scala del metodo delle equazioni lineari. Non sorprende che ci ritroviamo con le stesse equazioni di prima. Qualcos’altro da notare è la formazione triangolare nell’angolo in basso a sinistra della matrice finale. È logico che emerga questo schema perché gli 0 sono indicatori di una variabile eliminata e ogni variabile eliminata ci avvicina all’identificazione di un’equazione per la quale possiamo risolvere facilmente; questo a sua volta fa progredire la soluzione del sistema nel suo complesso. Rivisiteremo questo evento e ne fornirò una definizione più formale nel prossimo capitolo.
Riepilogo
In questo capitolo abbiamo imparato:
- Equazioni lineari: un’equazione con una o più variabili in cui il grado dell’equazione deve essere uguale a 1.
- Sistemi di equazioni lineari: una raccolta di equazioni lineari.
- Soluzioni di un sistema di una o più equazioni lineari: un sistema lineare non ha soluzioni, ha una soluzione unica o infinite soluzioni.
- Notazione matriciale: matrice rettangolare utilizzata in modo condensato per rappresentare un sistema lineare.
- Operazioni sulle righe: le operazioni di sostituzione, scambio e ridimensionamento ci consentono di trasformare una matrice in una che ha eliminato abbastanza variabili sconosciute da risolvere per il sistema.
- Risolvere un sistema lineare: un modo sistematico per trovare a) se esistono soluzioni per un dato sistema lineare e b) se esistono soluzioni, quali sono i loro valori esatti.
Appunti
*Se non diversamente specificato, tutte le immagini sono dell’autore dell’articolo.
* Piccola digressione: la parola quadratico deriva da qpiazza che è il participio passato della parola latina piazza che significa “fare quadrato.”; che rende omaggio alla sua laurea! (SRC)
*ℝ² è lo spazio di tutte le possibili coppie ordinate (x, y) sulla linea dei numeri reali, è rappresentato da un piano bidimensionale. ℝ² incapsula l’intero insieme dei numeri reali e l’insieme dei numeri reali è innumerevole infinito, il che significa che anche lo spazio ℝ² è infinito.
*Citazione per le operazioni sulle righe (origine)
Fonte: towardsdatascience.com


