Prefazione
Bentornati al terzo saggio della mia serie in corso sulle basi dell’algebra lineare, la matematica fondamentale dietro l’apprendimento automatico. Nel mio precedente articoloHo camminato attraverso le forme della matrice scaglione. Questo articolo esaminerà i vettori, le campate e le combinazioni lineari e collegherà queste nuove idee a ciò che abbiamo già imparato. Questo articolo sarebbe più utile ai lettori se letto insieme a Algebra lineare e le sue applicazioni di David C. Lay, Steven R. Lay e Judi J. McDonald. Considera questa serie come una risorsa complementare.
Sentiti libero di condividere pensieri, domande e critiche.
Vettori in ℝ², ℝ³ e ℝⁿ
Finora abbiamo imparato a conoscere le matrici che sono array di numeri, e se avessimo semplicemente un array (singolare) di numeri? Ecco il vettore: un tipo speciale di matrice con una dimensione di M X 1, dove m indica il numero di righe o voci nel vettore. Ricordiamo che la notazione per la dimensione della matrice è M X NDove M è uguale al numero di righe while N corrisponde al numero di colonne. Un vettore avrà sempre solo una colonna, ma un numero qualsiasi di righe.
L’insieme di tutti i vettori con due voci è ℝ². ℝ incapsula l’intero insieme dei numeri reali, quindi ha senso che ℝ² sia lo spazio bidimensionale di tutti i possibili punti (x, y) dei numeri reali.
I vettori possono essere in ℝ², ℝ³, ℝ⁴ … ℝⁿ, nota che la dimensione dello spazio vettoriale corrisponde al numero di voci nel vettore.
Probabilmente alla fine incontrerai il peculiare vettore zero (scritto semplicemente come 0), un vettore in cui tutte le sue voci sono zero. Sebbene possa sembrare un dettaglio minore, scopriremo in seguito che ha importanti implicazioni per alcune delle idee più importanti dell’algebra lineare.
Visualizzazione geometrica
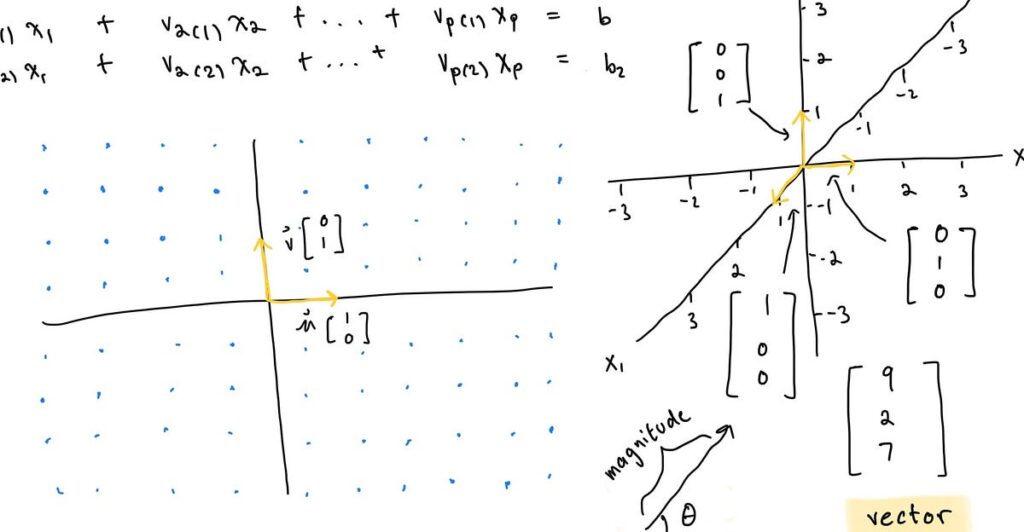
Fino ad ora, matrici e vettori sono stati descritti, spiegati e annotati matematicamente mentre i vettori in fisica sono descritti come quantità con grandezza e direzione. Entrambi sono ugualmente corretti; la visualizzazione grafica sottostante dei vettori in ℝ² unisce entrambe le definizioni di vettore.
È importante tenere presente che i vettori in ℝ² sono coppie ordinate e i vettori negli spazi vettoriali di dimensione superiore sono tuple ordinate (un elenco di numeri con un ordine definito). Due vettori possono avere esattamente gli stessi numeri delle loro voci, ma se l’ordine delle loro voci non è lo stesso, anche i vettori non sono gli stessi, come mostrato nel diagramma sopra.
È anche possibile visualizzare i vettori in ℝ³, aggiungiamo semplicemente un terzo asse poiché abbiamo una voce aggiuntiva. Oltre ℝ³, rappresentare graficamente i vettori diventa molto più contorto poiché diventa difficile immaginare spazi di dimensione superiore.
Proprietà algebriche dei vettori
Per tutti i vettori tu, v, w in ogni dato spazio vettoriale e scalare C E D: valgono le seguenti proprietà algebriche¹:
(i) commutativo*: tu + v = v + tu
(ii) associativo*: (tu + v) + w = w + (v + w)
(iii) identità additiva: tu + 0 = 0 + tu = tu
(iv) additivo inverso: tu + (-tu) = –tu + tu = 0
(v) distributiva con vettori: C(tu + v) = Ctu + Cv
(vi) distributiva con scalari: (C + D)tu = Ctu + Dtu
(vii) associativi con scalari: C(Dtu) = (CD)tu
Queste proprietà sono legate alle operazioni di addizione vettoriale e moltiplicazione scalare.
Per aggiungere due vettori, le voci corrispondenti vengono sommate per produrre la somma dei vettori. Ciò significa che la somma dei vettori per due vettori di dimensioni diverse non è definita. Per aggiungere due vettori, devono avere lo stesso numero di voci! Questa condizione deriva dal modo in cui viene eseguita l’addizione vettoriale.
Con moltiplicazione scalare, per un dato scalare C e vettore tuil multiplo scalare è Ctu dove ogni voce entra tu è stato moltiplicato per lo scalare C.
Queste due operazioni possono essere utilizzate insieme; e come scoprirai nella sezione successiva, sono combinati per formare un concetto centrale dell’algebra lineare: le combinazioni lineari.
Combinazioni lineari
Supponiamo di avere i vettori v₁, v₂, … vₐ in ℝⁿ e di avere degli scalari (noti anche come pesi) c₁, c₂, … cₐ, che possono essere qualsiasi numero reale, compreso lo zero. IL combinazione lineare è il vettore definito dalla somma dei multipli scalari, c₁v₁ + c₂v₂ + … + cₐvₐ. ²
In precedenza, abbiamo esplorato il concetto di esistenza in Algebra lineare dove, data una matrice, esiste almeno una soluzione? In altre parole, la forma a scaglioni ridotta/riga della matrice presenta un’incoerenza? Se è così, non esistono soluzioni. In caso contrario, almeno una soluzione lo fa. Questa domanda fondamentale sull’esistenza è legata a molte idee dell’algebra lineare e le combinazioni lineari non sono diverse.
Diciamo che un vettore B è una combinazione lineare di un insieme di vettori v₁, v₂, .. vₐₚ in Rⁿ, se esiste un insieme di pesi c₁, c₂, … cₐ (una soluzione) tale che c₁v₁ + c₂v₂ + … + cₐvₐ = B.
Per determinare se B è una combinazione lineare, possiamo utilizzare le operazioni di addizione vettoriale e moltiplicazione scalare per riorganizzare la nostra equazione di combinazione lineare: c₁v₁ + c₂v₂ + … + cₐvₐₚ = B in una notazione con la quale siamo diventati molto familiari. Questo processo di riarrangiamento fa anche luce sul perché esattamente capire se il vettore B è una combinazione lineare di un insieme di vettori è un problema di esistenza.
La spiegazione di cui sopra ha lo scopo di enfatizzare il motivo per cui il problema dell’esistenza e della riduzione delle righe della matrice è connesso a combinazioni lineari e dimostra l’idea in senso generale. Diamo un’occhiata a un esempio più specifico.
Nell’esempio sopra, dopo aver ridotto per righe la matrice aumentata alla forma a scaglioni di righe ridotte, abbiamo scoperto che una soluzione esiste davvero!
Consideriamo tuttavia il caso di una matrice aumentata in forma di scaglioni ridotti per righe con la riga (0, 0, … | B) Dove B ≠ 0, ciò significherebbe che il vettore B non può essere scritto come combinazione lineare di un insieme di vettori. In altre parole, il vettore B è fuori portata per il nostro insieme di vettori o (e questo è un bel passaggio alla prossima sezione) per il vettore B non è all’interno di arco dell’insieme dei vettori.
Arco di un insieme di vettori
L’insieme di tutte le possibili combinazioni lineari per i vettori v₁, v₂, … vₐ in ℝⁿ è indicato come il sottoinsieme di ℝⁿ compreso tra v₁, v₂, … vₐ. IL arco di vettori v₁, v₂, … vₐ è indicato come Span{v₁, v₂, … vₐ} ed è l’insieme di vettori che può essere scritto come c₁v₁ + c₂v₂ + … + cₐvₐ.³ Un altro modo di pensarci è che lo span contiene tutto i vettori che possono essere scritti come combinazione lineare dei vettori v₁, v₂, … vₐ.
Possiamo trovare lo span per un dato insieme di un numero qualsiasi di vettori. Supponiamo di avere un insieme di un vettore singolare, v₁. Gli Span{v₁} sarebbero quindi tutti i multipli scalari di v₁ perché l’unica operazione che può essere applicata in questo caso è la moltiplicazione scalare (sono necessari almeno due vettori per eseguire l’addizione dei vettori). Lo Span{v₁} contiene tutti i vettori che possono essere raggiunti da v₁.
Se dovessimo visualizzare l’intervallo, sarebbe una linea retta che passa per v₁ e l’origine perché con un solo vettore le combinazioni lineari (multipli di vettori) non possono cambiare direzione. Questo punto è ulteriormente illustrato nel diagramma seguente.
Considera l’estensione di due vettori in direzioni diverse in ℝ², quali sono le possibili combinazioni lineari che questi due vettori potrebbero formare? In altre parole, quali sono i vettori in ℝ² che possono essere scritti come combinazione lineare di questi due vettori?
Per il caso di cui sopra, dopo ulteriori indagini, sembra che tu E v abbraccia tutto ℝ²! Ciò significa che qualsiasi vettore in ℝ² può essere scritto come una combinazione lineare di tu E v. In un prossimo articolo esploreremo il concetto di indipendenza lineare che verrà utilizzato per dimostrarlo concretamente tu E v campata ℝ².
Conclusione
Vettori, combinazioni lineari e span ci portano un passo più in profondità nel rigoglioso campo dell’algebra lineare. Questi concetti fondamentali ci aiutano a comprendere la struttura degli spazi vettoriali e le relazioni tra diversi insiemi di vettori. Man mano che progrediamo, scoprirai che queste idee riaffiorano continuamente perché sono collegate ad altri concetti fondamentali. Allo stesso modo, spero che ti prenderai del tempo per pensare a come tutto ciò che abbiamo imparato finora (l’esistenza di soluzioni, le forme di scaglioni di fila) è profondamente connesso a questi nuovi concetti.
Riepilogo
In questo capitolo abbiamo appreso:
- Vettori in ℝ², ℝ³ e ℝⁿ: il vettore è un tipo speciale di matrice con una dimensione di M X 1. UN il vettore può avere un numero qualsiasi di voci ma solo una colonna. Abbiamo scoperto che è anche possibile avere un vettore zero, un vettore in cui tutti i suoi elementi sono zero.
- La visualizzazione geometrica dei vettori: i vettori possono essere rappresentati graficamente, il che aiuta a capire da dove provengono le idee di grandezza e direzione.
- Proprietà algebriche dei vettori: le seguenti proprietà algebriche dei vettori valgono per tutti i vettori e gli scalari; identità commutativa, associativa, additiva, inversa additiva, distributiva con vettori, distributiva con scalari e associativa con scalari.
- Combinazioni lineari: la combinazione lineare è il vettore definito dalla somma dei multipli scalari c₁v₁ + c₂v₂ + … + cₐvₐ. I pesi c₁, c₂, … cₐ possono essere qualsiasi scalare compreso zero.
- Span vettoriali: lo span dei vettori v₁, v₂, … vₐ è indicato come Span{v₁, v₂, … vₐ} ed è l’insieme dei vettori che può essere scritto come c₁v₁ + c₂v₂ + … + cₐvₐ.
Appunti
¹Proprietà algebriche dei vettori a cui si fa riferimento https://cs.brown.edu/stc/summer/94GeoTrans/94GeoTrans_17.html
²Definizione di combinazioni lineari a cui si fa riferimento da Algebra lineare e sue applicazioni 6a edizione di David C. Lay, Steven R. Lay e Judi J. McDonald
³Definizione di span a cui si fa riferimento da Linear Algebra and Its Applications 6th Edition di David C. Lay, Steven R. Lay e Judi J. McDonald.
*Tutte le immagini create dall’autore se non diversamente specificato.
*La proprietà associativa fa sì che nelle operazioni di addizione e moltiplicazione i numeri possano essere raggruppati in qualsiasi modo e il risultato rimarrà lo stesso. Ad esempio, (5 + 2) + 3 = 5 + (2 + 3) = 10 e (5 x 2) x 3 = 5 x (2 x 3) = 30.
*Commutativo significa che per le operazioni di addizione e moltiplicazione, i numeri possono essere sommati o moltiplicati in qualsiasi ordine e il risultato rimarrà lo stesso. Ad esempio, 5 + 2 = 2 + 5 = 7 e 5 x 2 = 2 x 5 = 10.
Fonte: towardsdatascience.com


