Algebra lineare 5: Indipendenza lineare | di tenzin migmar (t9nz) | Marzo 2024 | Intelligenza-Artificiale

Indice contenuti

Ax = 0 e dimostrare che un insieme di vettori è linearmente indipendente

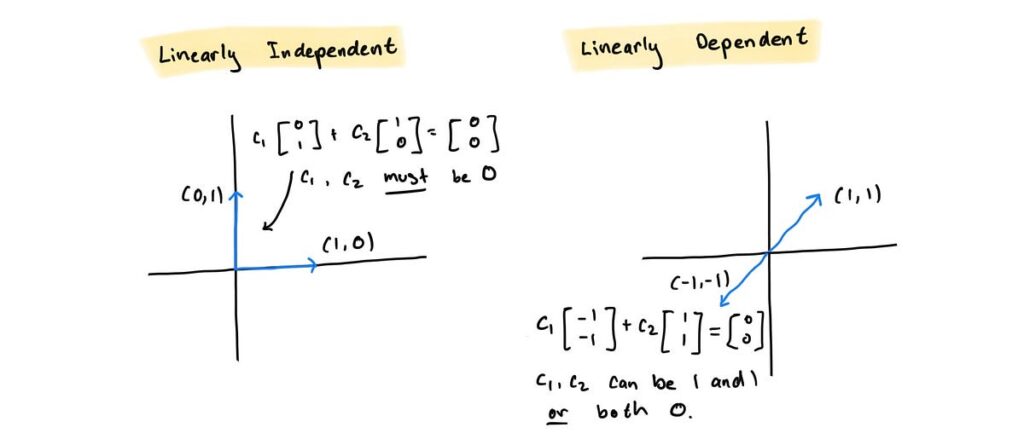
Prefazione

Bentornati alla quinta edizione della mia serie in corso sulle basi dell'algebra lineare, la matematica fondamentale dietro l'apprendimento automatico. Nel mio precedente articoloHo esaminato l'equazione della matrice Ax = B. Questo saggio indagherà l'importante concetto di indipendenza lineare e come si collega a tutto ciò che abbiamo imparato finora.

Questo articolo sarebbe più utile ai lettori se letto insieme a Algebra lineare e le sue applicazioni di David C. Lay, Steven R. Lay e Judi J. McDonald. Considera questa serie come una risorsa complementare.

Sentiti libero di condividere pensieri, domande e critiche.

Indipendenza lineare in ℝⁿ

In precedenza, abbiamo appreso dei prodotti di matrici e delle equazioni di matrici nel modulo UNX = B. Ne abbiamo parlato UNX = B ha una soluzione X Se B è una combinazione lineare dell'insieme di vettori (colonne) nella matrice UN.

Esiste un'equazione di matrice speciale nell'algebra lineare UNX = 0 che chiameremo sistema lineare omogeneo. UNX = 0 avrà sempre almeno una soluzione dove X = 0 che è chiamata soluzione banale perché è banalmente facile dimostrare che qualsiasi matrice UN moltiplicato per il 0 vettore X risulterà nel 0 vettore.

Ciò che ci interessa veramente sapere è se l'equazione di matrice UNX = 0 ha soltanto la soluzione banale. Se UNX = 0 ha solo la soluzione banale X = 0, allora l'insieme dei vettori che compongono le colonne di UN sono linearmente indipendenti. In altre parole: v₁ + c₂v₂ + … + cₐvₐ = 0 dove c₁, c₂, … cₐ devono essere tutti 0. Un modo diverso di pensare a questo è che nessuno dei vettori nell’insieme può essere scritto come una combinazione lineare di un altro .

D'altra parte, se esiste una soluzione dove X ≠ 0 allora l'insieme dei vettori è linearmente dipendente. Ne consegue che almeno uno dei vettori dell'insieme può essere scritto come combinazione lineare di un altro: c₁v₁ + c₂v₂ + … + cₐvₐ = 0 dove non tutti dove c₁, c₂, … cₐ uguale 0.

Un modo chiaro e intuitivo di pensare al concetto di indipendenza lineare è la domanda: riesci a trovare un insieme di pesi che collasserà la combinazione lineare di un insieme di vettori fino all'origine? Se un insieme di vettori è linearmente indipendente, allora 0 è l'unico peso che può essere applicato a ciascun vettore affinché la combinazione lineare sia uguale al vettore zero. Se i vettori sono linearmente dipendenti, allora esiste almeno un insieme di pesi diversi da zero tali che la combinazione lineare dei vettori sia zero.

Determinazione dell'indipendenza lineare

Per gli insiemi con un solo vettore, determinare l'indipendenza lineare è banale. Se il vettore è zero allora è linearmente dipendente. Questo perché qualsiasi peso diverso da zero moltiplicato per il vettore zero sarà uguale al vettore zero e quindi esistono infinite soluzioni per UNX = 0. Se il vettore non è il vettore zero, allora il vettore è linearmente indipendente poiché qualsiasi vettore moltiplicato per zero diventerà il vettore zero.

Se un insieme contiene due vettori, i vettori sono linearmente dipendenti se uno dei vettori è multiplo dell'altro. Altrimenti sono linearmente indipendenti.

Nel caso di insiemi con più di due vettori, sono coinvolti più calcoli. Lascia che i vettori formino le colonne della matrice UN e matrice di riduzione delle righe UN alla forma a scaglioni di fila ridotta. Se la forma a scaglioni di righe ridotte della matrice ha una voce pivot in ogni colonna, allora l'insieme dei vettori è linearmente indipendente. Altrimenti l'insieme dei vettori è linearmente dipendente. Perché è così? Consideriamo il processo di riduzione per righe di una matrice alla sua forma a scaglioni di righe ridotte. Eseguiamo una serie di operazioni elementari sulle righe come moltiplicare righe per costanti, scambiare righe, aggiungere una riga a un'altra alla ricerca di una matrice in una forma più semplice in modo che le sue proprietà sottostanti siano chiare mentre lo spazio delle soluzioni sia preservato.

Nel caso dell'indipendenza lineare, la qualità di avere un perno in ciascuna colonna indica che ciascun vettore gioca un ruolo principale in almeno una parte dell'equazione della combinazione lineare. Se ogni vettore contribuisce in modo indipendente al sistema lineare, allora nessun vettore può essere espresso come combinazione lineare degli altri e quindi il sistema è linearmente indipendente. Al contrario, se in RREF è presente una colonna senza una voce pivot, significa che la variabile (o vettore) corrispondente è una variabile dipendente e può essere espressa in termini di altri vettori. In altre parole, esiste una ridondanza nel sistema, che indica una dipendenza lineare tra i vettori.

Un modo conciso per riassumere questa idea coinvolge il rango di una matrice. Il rango è il numero massimo di colonne linearmente indipendenti in una matrice e quindi ne consegue che il rango è uguale al numero di perni nella forma a scaglioni di righe ridotte.

Se il numero di colonne di una matrice è uguale al rango, la matrice è linearmente indipendente. Altrimenti la matrice è linearmente dipendente.

Indipendenza lineare con Numpy

Tentare di eseguire calcoli manualmente è un esercizio utile per comprendere meglio l'indipendenza lineare, ma un approccio più pratico sarebbe quello di utilizzare le funzionalità integrate nella libreria Numpy sia per testare l'indipendenza lineare sia per derivare lo spazio delle soluzioni per UNX = 0 di una data matrice.

Possiamo avvicinarci al controllo se una matrice è linearmente indipendente utilizzando il rango. Come accennato in precedenza, una matrice è linearmente indipendente se il suo rango è uguale al numero di colonne, quindi il nostro codice sarà scritto attorno a questo criterio.