La messa a punto di modelli pre-addestrati di grandi dimensioni è impegnativa dal punto di vista computazionale, e spesso comporta la regolazione di milioni di parametri. Questo approccio tradizionale di messa a punto, sebbene efficace, richiede notevoli risorse computazionali e tempo, ponendo un collo di bottiglia per l’adattamento di questi modelli a compiti specifici. LoRA ha presentato una soluzione efficace a questo problema scomponendo la matrice di aggiornamento durante il perfezionamento. Per studiare LoRA, iniziamo rivisitando prima il perfezionamento tradizionale.
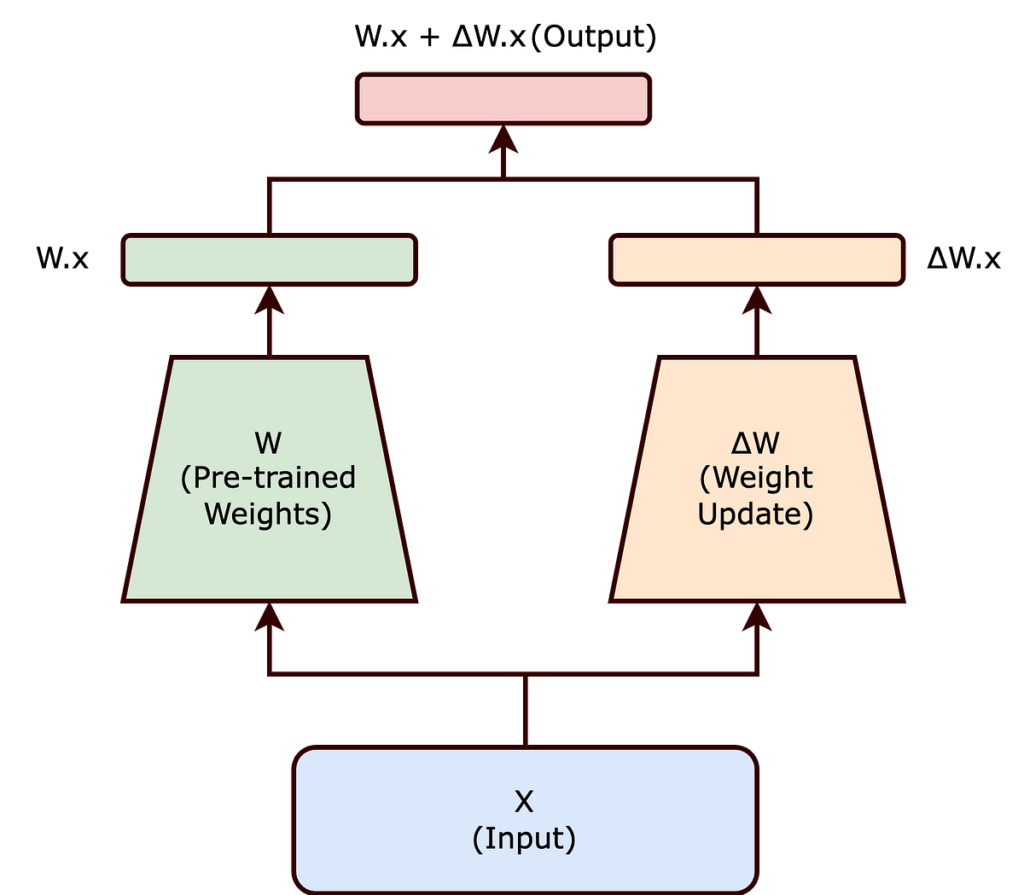
Nella messa a punto tradizionale, modifichiamo i pesi di una rete neurale pre-addestrata per adattarla a un nuovo compito. Questo aggiustamento comporta l’alterazione della matrice dei pesi originari (W) della rete. Le modifiche apportate a ( W ) durante la messa a punto sono rappresentate collettivamente da ( Δ W ), in modo tale che i pesi aggiornati possano essere espressi come ( W + Δ W ).
Ora, invece di modificare direttamente (W), l’approccio LoRA cerca di scomporre (Δ W). Questa scomposizione è un passo cruciale nella riduzione del sovraccarico computazionale associato alla messa a punto di modelli di grandi dimensioni.
L’ipotesi del rango intrinseco suggerisce che cambiamenti significativi nella rete neurale possono essere catturati utilizzando una rappresentazione di dimensione inferiore. In sostanza, si presuppone che non tutti gli elementi di ( Δ W ) siano ugualmente importanti; invece, un sottoinsieme più piccolo di questi cambiamenti può effettivamente incapsulare gli aggiustamenti necessari.
Basandosi su questa ipotesi, LoRA propone di rappresentare ( Δ W ) come il prodotto di due matrici più piccole, ( A ) e ( B ), di rango inferiore. La matrice dei pesi aggiornata (W’) diventa quindi:
( W’ = W + BA )
In questa equazione, ( W ) rimane congelato (cioè non viene aggiornato durante l’addestramento). Le matrici (B) e (A) sono di dimensionalità inferiore, con il loro prodotto (BA) che rappresenta un’approssimazione di basso rango di (Δ W).
Scegliendo che le matrici ( A ) e ( B ) abbiano un rango inferiore ( r ), il numero di parametri addestrabili viene significativamente ridotto. Ad esempio, se ( W ) è una matrice ( dxd ), tradizionalmente l’aggiornamento ( W ) coinvolgerebbe i parametri ( d² ). Tuttavia, con (B) e (A) rispettivamente di dimensioni (dxr) e (rxd), il numero totale di parametri si riduce a (2dr), che è molto più piccolo quando (r << d).
La riduzione del numero di parametri addestrabili, ottenuta attraverso il metodo Low-Rank Adaptation (LoRA), offre numerosi vantaggi significativi, in particolare durante la messa a punto di reti neurali su larga scala:
- Impronta di memoria ridotta: LoRA riduce le esigenze di memoria diminuendo il numero di parametri da aggiornare, aiutando nella gestione di modelli su larga scala.
- Formazione e adattamento più rapidi: semplificando le richieste computazionali, LoRA accelera la formazione e la messa a punto di modelli di grandi dimensioni per nuove attività.
- Fattibilità per hardware più piccolo: il numero inferiore di parametri di LoRA consente la messa a punto di modelli sostanziali su hardware meno potente, come GPU o CPU modeste.
- Adattamento a modelli più grandi: LoRA facilita l’espansione dei modelli di intelligenza artificiale senza un corrispondente aumento delle risorse computazionali, rendendo più pratica la gestione delle dimensioni crescenti dei modelli.
Nel contesto di LoRA, il concetto di rango gioca un ruolo fondamentale nel determinare l’efficienza e l’efficacia del processo di adattamento. Sorprendentemente, l’articolo evidenzia il rango delle matrici UN E B può essere sorprendentemente basso, a volte fino a uno.
Sebbene il documento LoRA mostri prevalentemente esperimenti nell’ambito dell’elaborazione del linguaggio naturale (NLP), l’approccio sottostante dell’adattamento di basso rango ha un’ampia applicabilità e potrebbe essere efficacemente impiegato nell’addestramento di vari tipi di reti neurali in diversi domini.
L’approccio di LoRA alla scomposizione ( Δ W ) in un prodotto di matrici di rango inferiore bilancia efficacemente la necessità di adattare grandi modelli pre-addestrati a nuovi compiti mantenendo l’efficienza computazionale. Il concetto di rango intrinseco è fondamentale per questo equilibrio, garantendo che l’essenza della capacità di apprendimento del modello sia preservata con un numero significativamente inferiore di parametri.
Fonte: towardsdatascience.com


