Ogni giorno e ogni minuto, Uber riceve molteplici richieste nel proprio mercato. Ogni evento avviene in una località specifica, ad esempio un ciclista chiede un passaggio in una località e un conducente accetta il viaggio in una località vicina. Per ricavare informazioni e approfondimenti dai dati, ad esempio impostando prezzi dinamici basati sulla domanda, è necessario analizzare i dati di un'intera città. Ma poiché le città sono geograficamente molto diverse, questa analisi deve avvenire con granularità fine. Con il sistema a griglia esagonale H3, ciascun punto dati può essere raggruppato in un'area o cella esagonale, quindi un Uber può calcolare l'offerta e la domanda per l'aumento dei prezzi su ciascun esagono in tutte le città in cui offrono servizi. Gli esagoni sono disponibili in diverse dimensioni, quindi è necessario scegliere la risoluzione che meglio si adatta allo scopo dell'analisi.
Tecnicamente si potrebbe costruire un sistema di griglia globale utilizzando qualsiasi tipo di elemento costitutivo che faciliti una piastrellatura completa in tutto il globo 3D. Ad esempio si potrebbero usare triangoli (3 lati) o quadrati (4 lati) invece di esagoni (6 lati) per coprire l'intera Terra. Tuttavia, l’uso degli esagoni presenta molti vantaggi. Ad esempio, il punto centrale di un triangolo ne ha tre e un quadrato ha due distanze diverse dai centri dei suoi vicini mentre il punto centrale di un esagono ha la stessa distanza da tutti i suoi vicini, il che lo rende un sistema conveniente per approssimare i raggi (vedi immagine sotto).
Tuttavia, il mondo non può essere diviso completamente in esagoni, quindi sono necessari anche pochi pentagoni (cinque lati) (12 per l'esattezza, per ciascuna risoluzione). I pentagoni introducono discontinuità nella rete ma spesso sono posizionati lontano dalla terra e questo causa problemi soprattutto per l'analisi dei dati marini. Nonostante la presenza di alcuni pentagoni, la griglia esagonale offre il vantaggio di fornire elementi costitutivi di dimensioni relativamente uniformi sulla superficie sferica 3D. Nel caso in cui si voglia saperne di più sulla geometria di una griglia esagonale, ecco una buona fonte per questo. Si noti che la definizione delle regioni esagonali è altamente arbitraria e non seguono alcuna caratteristica naturale come laghi, fiumi, montagne o confini nazionali.
La libreria H3 è open source, disponibile su GitHub e scritta in C. Ha collegamenti disponibili su più linguaggi, ad esempio su Python, C, Java e Javascript. H3 è dotato di un sistema di indicizzazione gerarchico che lo rende molto efficiente. È possibile esaminare ulteriormente gli esagoni utilizzando un online Visualizzatore dati esagonale H3. La tabella seguente riassume le proprietà delle 16 diverse risoluzioni fornite da H3.
Successivamente, introdurremo alcune delle funzionalità più importanti della libreria H3.
In questo articolo utilizzeremo il sistema esagonale H3 per raggruppare i dati sulla posizione in esagoni. È possibile trovare la documentazione della libreria H3 Qui. Esistono due versioni principali di questa libreria, le versioni 3 e 4, e nei nostri quaderni utilizzeremo la versione 3.7.6. Tieni presente che esistono differenze significative nei nomi delle funzioni tra la versione 3.x e 4.x, come elencato in Qui.
Il pacchetto H3 Python è facile da installare, ad esempio con pip:
pip install h3
Se vuoi specificare quale versione vuoi utilizzare, aggiungi lì il numero di versione, ad esempio h3==3.7.6. Quindi importa H3 sul tuo notebook Python con
import h3
Successivamente, introdurremo alcune delle funzioni più importanti della libreria H3.
Indice esagonale
H3 utilizza un sistema di indicizzazione gerarchico, che trasforma le coppie di latitudine e longitudine in un indice H3 a 64 bit che identifica ciascuna cella della griglia. Date le coordinate (latitudine e longitudine) e con la risoluzione selezionata, otteniamo l'indice esagonale:
# Version 3.X:
hexagon_index = h3.geo_to_h3(lat, lng, resolution)# Version 4.X:
hexagon_index = h3.latlng_to_cell(lat, lng, resolution)
Per esempio
h3.geo_to_h3(60.169833, 24.938163, 6)
restituisce l'indice '861126d37ffffff'. Se vuoi, puoi usare an visualizzatore di dati esagonali H3 online per verificare dove si trova questo esagono.
Pertanto, quando conosciamo le coordinate precise di un punto dati, possiamo determinarne l'indice esagonale a varie risoluzioni e associarlo ad esagoni di diverse dimensioni.
Confini dell'esagono
Per utilizzare gli esagoni nei nostri grafici, dobbiamo determinare i confini dell'esagono dall'indice esagonale. Tieni presente che le coordinate in alcuni sistemi sono presentate come (lng, lat), mentre in altri seguono il formato (lat, lng). L'opzione geo_json=True/False ti consente di scambiare queste coordinate.
# Version 3.X:
boundary = h3.h3_to_geo_boundary(hexagon_index, geo_json = False)# Version 4.X:
boundary = h3.cell_to_boundary(hexagon_index, geo_json = False)
Per esempio
h3.h3_to_geo_boundary('861126d37ffffff', geo_json = False)# Returns:
((60.15652369744344, 24.856525761155346),
(60.13498207546084, 24.895664284494664),
(60.14431977678549, 24.948769321085937),
(60.175221029708474, 24.962796993345798),
(60.19677983831024, 24.92362795620145),
(60.187420192445906, 24.870461733016352))
Queste sei coppie di coordinate corrispondono ai punti iniziale e finale dei bordi dell'esagono.
Esagoni vicini
A volte dobbiamo identificare i vicini di un esagono specifico, o “kring” attorno all'esagono. Con k=0 la funzione restituisce l'indice di origine, con k=1 restituisce l'indice di origine e tutti gli indici vicini, e con k=2 restituisce l'indice di origine, i suoi indici vicini e prossimi e così via .
# Version 3.X:
kring = h3.k_ring(hexagon_index, k)# Version 4.X:
kring = h3.grid_disk(hexagon_index, k)
Inoltre esiste una funzione che può essere utilizzata per calcolare la distanza della griglia tra due celle:
# Version 3.X:
kring = h3.h3_distance(hexagon_index_a, hexagon_index_a)# Version 4.X:
kring = h3.grid_distance(hexagon_index_a, hexagon_index_a)
Possiamo utilizzare queste funzioni nel modo seguente:
# Nearest neighbours of the hexagon:
h3.k_ring('861126d37ffffff', 1)# Returns:
{'86089969fffffff',
'86089ba4fffffff',
'86089ba6fffffff',
'861126d07ffffff',
'861126d17ffffff',
'861126d27ffffff',
'861126d37ffffff'}
# Distance between two hexagons:
h3.h3_distance('861126d37ffffff', '86089ba4fffffff')
# Returns
1
Tracciare gli esagoni
Esistono diversi modi per tracciare gli esagoni su una mappa, ma alcuni di essi sono piuttosto rigidi, richiedono molto tempo e non sono ben documentati. Per semplicità, utilizziamo principalmente matplotlib per le visualizzazioni, ma sperimentiamo e acquisiamo anche screenshot delle visualizzazioni con mappe folium. Maggiori dettagli su questi metodi di tracciamento possono essere trovati nel repository GitHub.
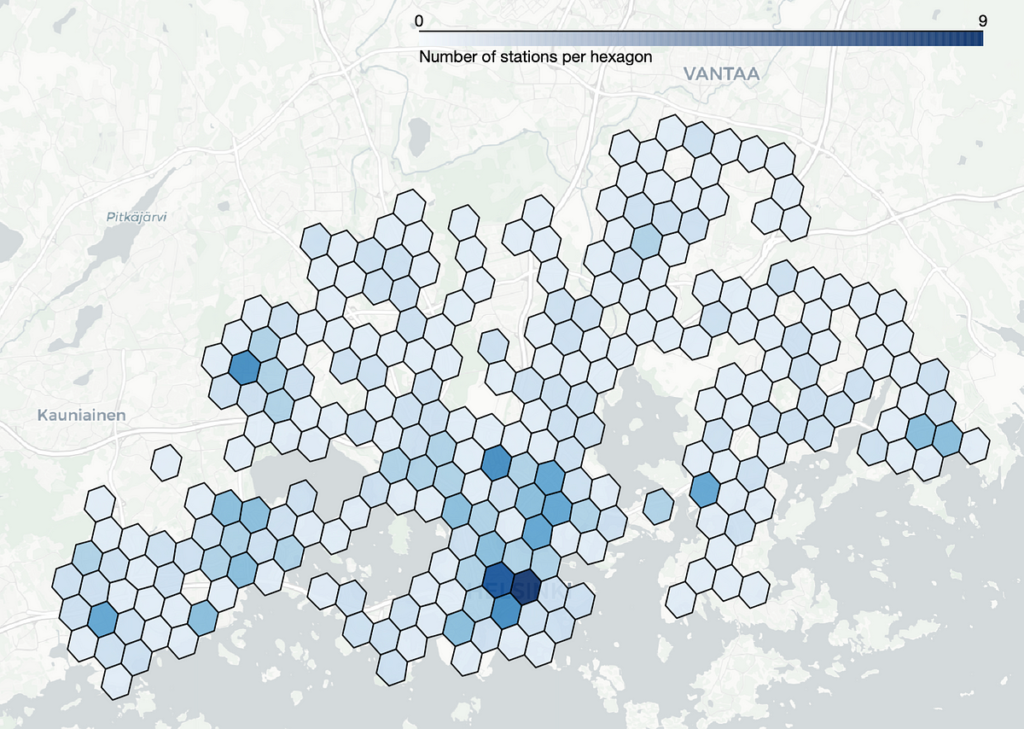
A sinistra nella figura sopra usiamo matplotlib per tracciare gli esagoni. Utilizziamo la libreria GADM per recuperare il multipoligono che rappresenta la regione di Helsinki e tracciarlo con il colore verde. Usiamo il blu sullo sfondo per rappresentare gli specchi d'acqua. Inoltre, includiamo un indicatore che indica il centro di Helsinki sulla mappa. Gli esagoni possono essere facilmente renderizzati utilizzando la funzione plot_polygon dalla libreria Shapely e i punti dati possono essere aggiunti al grafico utilizzando il grafico a dispersione. Ciò rende la trama molto semplice e veloce.
Abbiamo anche sperimentato altri metodi di plottaggio, come l'utilizzo delle mappe folium che ci consentono di creare una mappa HTML interattiva che ci consente di ingrandire e rimpicciolire la mappa. A destra nella figura sopra mostriamo uno screenshot di tale mappa. Anche se il risultato è esteticamente gradevole, aggiungere nuove funzionalità (come barre di colore o mappe di calore) alla mappa richiede molto tempo, quindi non è lo strumento migliore per l'analisi esplorativa dei dati. Il taccuino per tracciare le mappe interattive del foglio può essere trovato qui.
Fonte: towardsdatascience.com


