Eseguiamo il confronto dei modelli utilizzando the loo pacchetto (9, 10) per la convalida incrociata “leave-one-out”. Per un approccio alternativo utilizzando i criteri WAIC (11) Ti consiglio di leggere Questo post pubblicato anche da Redattori di TDS.
loo(Ordinal_Fit, Ordinal_Fit2)
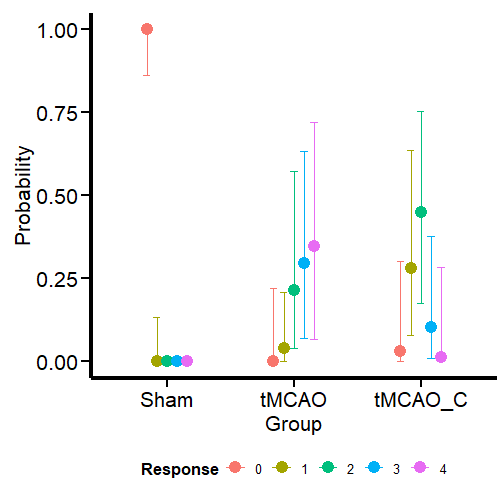
Con questo schema, i modelli hanno prestazioni molto simili. In effetti, il primo modello è leggermente migliore per le previsioni fuori campione. Tenere conto della varianza non è stato di grande aiuto in questo caso particolare, dove (forse) fare affidamento su informazioni a priori può sbloccare il passaggio successivo dell’inferenza scientifica.
Apprezzerei i tuoi commenti o feedback per farmi sapere se questo viaggio ti è stato utile. Se desideri più contenuti di qualità sulla scienza dei dati e altri argomenti, potresti prendere in considerazione l'idea di diventare un membro medio.
In futuro potresti trovare una versione aggiornata di questo post sul mio Sito GitHub.
1.M. Bieber, J. Gronewold, A.-C. Scharf, MK Schuhmann, F. Langhauser, S. Hopp, S. Mencl, E. Geuss, J. Leinweber, J. Guthmann, TR Doeppner, C. Kleinschnitz, G. Stoll, P. Kraft, DM Hermann, Validità e affidabilità dei punteggi neurologici nei topi esposti all'occlusione dell'arteria cerebrale media. Colpo. 502875–2882 (2019).
2. P.-C. Bürkner, M. Vuorre, Modelli di regressione ordinale in psicologia: un tutorial. Progressi nei metodi e nelle pratiche delle scienze psicologiche. 277–101 (2019).
3. G. Gigerenzer, Statistiche insensate. Il giornale di socioeconomia. 33587–606 (2004).
4. P.-C. Bürkner, Brms: un pacchetto r per modelli multilivello bayesiani che utilizzano stan. 80 (2017), doi:10.18637/jss.v080.i01.
5. H. Wickham, M. Averick, J. Bryan, W. Chang, LD McGowan, R. François, G. Grolemund, A. Hayes, L. Henry, J. Hester, M. Kuhn, TL Pedersen, E. Miller, SM Bache, K. Müller, J. Ooms, D. Robinson, DP Seidel, V. Spinu, K. Takahashi, D. Vaughan, C. Wilke, K. Woo, H. Yutani, Benvenuti nel tidyverse. 41686 (2019).
6. Makowski D, Ben-Shachar MS, Lüdecke D, bayestestR: Descrivere gli effetti e la loro incertezza, esistenza e significato all'interno del quadro bayesiano. 41541 (2019).
7. RV Lenth, Emmeans: medie marginali stimate, ovvero medie dei minimi quadrati (2023) (disponibile su https://CRAN.R-project.org/package=emmeans).
8. R. McElreath, Ripensamento statistico (Chapman; Hall/CRC, 2020; http://dx.doi.org/10.1201/9780429029608).
9. A. Vehtari, J. Gabry, M. Magnusson, Y. Yao, P.-C. Bürkner, T. Paananen, A. Gelman, Loo: Efficiente validazione incrociata “leave-one-out” e WAIC per modelli bayesiani (2022) (disponibile su https://mc-stan.org/loo/).
10. A. Vehtari, A. Gelman, J. Gabry, Valutazione pratica del modello bayesiano utilizzando la convalida incrociata “leave-one-out” e WAIC. Statistica e informatica. 271413–1432 (2016).
11. A. Gelman, J. Hwang, A. Vehtari, Comprensione dei criteri di informazione predittiva per i modelli bayesiani. Statistica e informatica. 24997–1016 (2013).
Fonte: towardsdatascience.com


