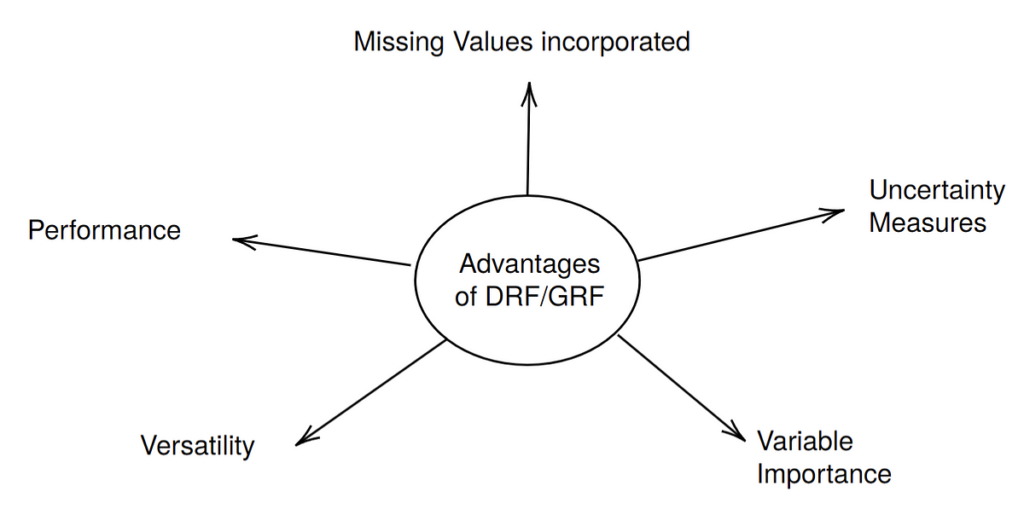
In termini di tempistiche di apprendimento automatico, le foreste casuali (RF), introdotte nell’articolo fondamentale di Breimann ((1)), sono antiche. Nonostante la loro età, continuano a stupire per le loro prestazioni e sono oggetto di ricerca attiva. L’obiettivo di questo articolo è quello di evidenziare quale versatile strumento siano diventati i metodi Random Forest, concentrandosi su Foresta casuale generalizzata (GRF) E Foresta casuale distribuzionale (DRF).
In breve, l’idea principale alla base di entrambi i metodi è che i pesi implicitamente prodotti da RF possono essere utilizzati per stimare obiettivi diversi dall’aspettativa condizionale. L’idea del GRF è quella di utilizzare una foresta casuale con un criterio di suddivisione adattato all’obiettivo che si ha in mente (ad esempio, media condizionale, quantili condizionali o effetto del trattamento condizionale). L’idea del DRF è quella di adattare il criterio di suddivisione in modo tale da poter stimare l’intera distribuzione condizionale. Da questo oggetto è possibile derivare molti target diversi in una seconda fase. In effetti, in questo articolo parlo principalmente di DRF, poiché ho più familiarità con questo metodo ed è un po’ più snello (solo una foresta deve essere adattata per un’ampia gamma di obiettivi). Tuttavia tutti i vantaggi, indicati nella figura sopra, valgono anche per GRF ed infatti il pacchetto DRF in R è costruito sulla base implementazione professionale del GRF. Inoltre, il fatto che il criterio di suddivisione delle foreste GRF sia adattato all’obiettivo significa che possono avere prestazioni migliori rispetto a DRF. Ciò è particolarmente vero per il binario Ydove dovrebbe essere usato probability_forests(). Quindi, anche se parlo principalmente di DRF, GRF dovrebbe essere tenuto presente in questo articolo.
L’obiettivo di questo articolo è fornire una panoramica con collegamenti a letture più approfondite nelle sezioni corrispondenti. Esamineremo ciascuno dei punti nella figura sopra in senso orario, faremo riferimento agli articoli corrispondenti e lo evidenzieremo con un piccolo esempio. Per prima cosa riassumo rapidamente i collegamenti più importanti a ulteriori letture di seguito:
Versatilità/Prestazioni: Articolo medio e documenti originali (DRF/GRF)
Valori mancanti incorporati: Articolo medio
Misure di incertezza: Articolo medio
Importanza variabile: Articolo medio
L’esempio
Prendiamo X_1, X_2, X_4, …, X_10 uniforme indipendentemente tra (-1,1) e crea dipendenza tra X_1 E X_3 prendendo X_3=X_1 + errore uniforme. Quindi simuliamo Y COME
## Load packages and functions needed
library(drf)
library(mice)
source("drfnew_v2.R")
## The function drfnew_v2.R is available below, or on
## https://github.com/JeffNaef/drfupdate## Set parameters
set.seed(10)
n<-1000
##Simulate Data that experiences both a mean as well as sd shift
# Simulate from X
x1 <- runif(n,-1,1)
x2 <- runif(n,-1,1)
x3 <- x1+ runif(n,-1,1)
X0 <- matrix(runif(7*n,-1,1), nrow=n, ncol=7)
Xfull <- cbind(x1,x2, x3, X0)
colnames(Xfull)<-paste0("X", 1:10)
# Simulate dependent variable Y
Y <- as.matrix(rnorm(n,mean = 0.8*(x1 > 0), sd = 1 + 1*(x2 > 0)))
##Also add MAR missing values using ampute from the mice package
X<-ampute(Xfull)$amp
head(cbind(Y,X))
Y X1 X2 X3 X4 X5
1 -3.0327466 -0.4689827 0.06161759 0.27462737 NA -0.624463079
2 1.2582824 -0.2557522 0.36972181 NA -0.04100963 0.009518047
3 -0.8781940 0.1457067 -0.23343321 NA -0.64519687 -0.945426305
4 3.1595623 0.8164156 0.90997600 0.69184618 -0.20573331 -0.007404298
5 1.1176545 -0.5966361 NA -1.21276055 0.62845399 0.894703422
6 -0.4377359 0.7967794 -0.92179989 -0.03863182 0.88271415 -0.237635732
X6 X7 X8 X9 X10
1 -0.9290009 0.5401628 0.39735433 -0.7434697 0.8807558
2 -0.2885927 0.3805251 -0.09051334 -0.7446170 0.9935311
3 -0.5022541 0.3009541 0.29424395 0.5554647 -0.5341800
4 0.7583608 -0.8506881 0.22758566 -0.1596993 -0.7161976
5 -0.3640422 0.8051613 -0.46714833 0.4318039 -0.8674060
6 -0.3577590 -0.7341207 0.85504668 -0.6933918 0.4656891
Si noti che con la funzione amputare da pacchetto topiabbiamo messo Mancante non casuale (MAR) valori mancanti attivati X evidenziare la capacità di GRF/DRF di gestire i valori mancanti. Inoltre, solo nel processo di cui sopra X_1 E X_2 sono rilevanti per la previsione Ytutte le altre variabili sono variabili di “rumore”. Un’impostazione così “sparsa” potrebbe effettivamente essere comune nei set di dati della vita reale.
Scegliamo ora un punto di prova per questo esempio che utilizzeremo in tutto:
x<-matrix(c(0.2, 0.4, runif(8,-1,1)), nrow=1, ncol=10)
print(x)(,1) (,2) (,3) (,4) (,5) (,6) (,7) (,8)
(1,) 0.2 0.4 0.7061058 0.8364877 0.2284314 0.7971179 0.78581 0.5310279
(,9) (,10)
(1,) -0.5067102 0.6918785
Versatilità
DRF stima la distribuzione condizionale P_{Y|X=X} sotto forma di pesi semplici:
Da questi pesi è possibile calcolare un’ampia gamma di obiettivi oppure utilizzarli per simulare la distribuzione condizionale. Un buon riferimento per la sua versatilità è l’originale ricerca articolodove sono stati utilizzati molti esempi, così come i corrispondenti articolo medio.
Nell’esempio, simuliamo prima da questa distribuzione:
DRF<-drfCI(X=X, Y=Y, B=50,num.trees=1000, min.node.size = 5)
DRFpred<-predictdrf(DRF, newdata=x)## Sample from P_{Y| X=x}
Yxs<-Y(sample(1:n, size=n, replace = T, DRFpred$weights(1,)))
hist(Yxs, prob=T)
z<-seq(-6,7,by=0.01)
d<-dnorm(z, mean=0.8 * (x(1) > 0), sd=(1+(x(2) > 0)))
lines(z,d, col="darkred" )
Il grafico mostra i prelievi approssimativi dalla distribuzione condizionale sovrapposti alla densità reale in rosso. Ora lo usiamo per stimare il aspettativa condizionale e il quantili condizionali (0,05, 0,95). A X:
# Calculate quantile prediction as weighted quantiles from Y
qx <- quantile(Yxs, probs = c(0.05,0.95))# Calculate conditional mean prediction
mux <- mean(Yxs)
# True quantiles
q1<-qnorm(0.05, mean=0.8 * (x(1) > 0), sd=(1+(x(2) > 0)))
q2<-qnorm(0.95, mean=0.8 * (x(1) > 0), sd=(1+(x(2) > 0)))
mu<-0.8 * (x(1) > 0)
hist(Yxs, prob=T)
z<-seq(-6,7,by=0.01)
d<-dnorm(z, mean=0.8 * (x(1) > 0), sd=(1+(x(2) > 0)))
lines(z,d, col="darkred" )
abline(v=q1,col="darkred" )
abline(v=q2, col="darkred" )
abline(v=qx(1), col="darkblue")
abline(v=qx(2), col="darkblue")
abline(v=mu, col="darkred")
abline(v=mux, col="darkblue")
Allo stesso modo, molti obiettivi possono essere calcolati con GRF, solo che in questo caso per ciascuno di questi due obiettivi dovrebbe essere adatta una foresta diversa. In particolare, regression_forest() per l’aspettativa condizionale e quantile_foresta() per i quantili.
Ciò che il GRF non può fare è affrontare obiettivi multivariati, cosa possibile anche con il DRF.
Prestazione
Nonostante tutto il lavoro svolto su nuovi e potenti metodi (non parametrici), come le reti neurali, i metodi basati sugli alberi sono costantemente in grado di battere i concorrenti sui dati tabulari. Vedi ad esempio questo carta affascinanteo questo vecchio documento sul forza della RF nella classificazione.
Per essere onesti, con la regolazione dei parametri, metodi dell’albero potenziatocome XGboost, spesso prendono l’iniziativa, almeno quando si tratta di previsione classica (che corrisponde alla stima delle aspettative condizionate). Ciononostante, le prestazioni robuste che i metodi RF tendono ad avere senza alcuna regolazione sono notevoli. Inoltre, si è lavorato anche per migliorare le prestazioni delle foreste casuali, ad esempio the Approccio Random Forest coperto.
Valori mancanti incorporati
“Mancante incorporato nel criterio degli attributi” (MIA) da questo articolo è un’idea molto semplice ma molto potente che consente ai metodi basati su alberi di gestire i dati mancanti. Questo è stato implementato nel pacchetto GRF R e quindi è disponibile anche in DRF. I dettagli sono spiegati anche qui articolo medio. Per quanto semplice sia il concetto, funziona molto bene nella pratica: nell’esempio sopra, DRF non ha avuto problemi a gestire una sostanziale mancanza di MAR nei dati di addestramento X (!)
Misure di incertezza
Come statistico non voglio solo stime puntuali (anche di una distribuzione), ma anche una misura di incertezza della stima dei miei parametri (anche se il “parametro” è tutta la mia distribuzione). Risulta che un semplice sottocampionamento aggiuntivo integrato in DRF/GRF consente una quantificazione dell’incertezza di principio per campioni di grandi dimensioni. Da qui deriva la teoria che sta dietro a ciò nel caso del DRF ricerca articoloma lo spiego anche in questo articolo medio. GRF ha tutta la teoria in carta originale.
Lo adattiamo all’esempio sopra:
# Calculate uncertainty
alpha<-0.05
B<-length(DRFpred$weightsb)
qxb<-matrix(NaN, nrow=B, ncol=2)
muxb<-matrix(NaN, nrow=B, ncol=1)
for (b in 1:B){
Yxsb<-Y(sample(1:n, size=n, replace = T, DRFpred$weightsb((b))(1,)))
qxb(b,) <- quantile(Yxsb, probs = c(0.05,0.95))
muxb(b) <- mean(Yxsb)
}
CI.lower.q1 <- qx(1) - qnorm(1-alpha/2)*sqrt(var(qxb(,1)))
CI.upper.q1 <- qx(1) + qnorm(1-alpha/2)*sqrt(var(qxb(,1)))CI.lower.q2 <- qx(2) - qnorm(1-alpha/2)*sqrt(var(qxb(,2)))
CI.upper.q2 <- qx(2) + qnorm(1-alpha/2)*sqrt(var(qxb(,2)))
CI.lower.mu <- mux - qnorm(1-alpha/2)*sqrt(var(muxb))
CI.upper.mu <- mux + qnorm(1-alpha/2)*sqrt(var(muxb))
hist(Yxs, prob=T)
z<-seq(-6,7,by=0.01)
d<-dnorm(z, mean=0.8 * (x(1) > 0), sd=(1+(x(2) > 0)))
lines(z,d, col="darkred" )
abline(v=q1,col="darkred" )
abline(v=q2, col="darkred" )
abline(v=qx(1), col="darkblue")
abline(v=qx(2), col="darkblue")
abline(v=mu, col="darkred")
abline(v=mux, col="darkblue")
abline(v=CI.lower.q1, col="darkblue", lty=2)
abline(v=CI.upper.q1, col="darkblue", lty=2)
abline(v=CI.lower.q2, col="darkblue", lty=2)
abline(v=CI.upper.q2, col="darkblue", lty=2)
abline(v=CI.lower.mu, col="darkblue", lty=2)
abline(v=CI.upper.mu, col="darkblue", lty=2)
Come si può vedere dal codice sopra, essenzialmente abbiamo B sottoalberi che possono essere utilizzati per calcolare di volta in volta la misura. Da questi B campioni di media e quantili, possiamo quindi calcolare le varianze e utilizzare un’approssimazione normale per ottenere gli intervalli di confidenza (asintotici) visualizzati nella linea tratteggiata nella Figura. Ancora una volta, tutto ciò può essere fatto nonostante i valori mancanti X(!)
Importanza variabile
Un ultimo aspetto importante delle foreste casuali sono le misure di importanza variabile calcolate in modo efficiente. Sebbene le misure tradizionali siano in qualche modo ad hoc, per la RF tradizionale e per la DRF sono ora disponibili misure basate su principi, come spiegato in questo documento. articolo medio. Per RF, il metodo Sobol-MDA identifica in modo affidabile le variabili più importanti per la stima delle aspettative condizionate, mentre per DRF, MMD-MDA identifica le variabili più importanti per la stima della distribuzione complessiva. Come discusso nell’articolo, utilizzando l’idea di Foreste casuali previstequeste misure possono essere implementate in modo molto efficiente. Lo dimostriamo nell’esempio con un’implementazione meno efficiente della misura di importanza variabile MMD:
## Variable importance for conditional Quantile Estimation## For the conditional quantiles we use a measure that considers the whole distribution,
## i.e. the MMD based measure of DRF.
MMDVimp <- compute_drf_vimp(X=X,Y=Y, print=F)
sort(MMDVimp, decreasing = T)
X2 X1 X8 X6 X3 X10
0.852954299 0.124110913 0.012194176 0.009578300 0.008191663 0.007517931
X9 X7 X5 X4
0.006861688 0.006632175 0.005257195 0.002401974
Eccoli entrambi X_1 E X_2 sono correttamente identificati come la variabile più rilevante quando si tenta di stimare la distribuzione. Sorprendentemente, nonostante la dipendenza di X_3 E X_1la misura lo quantifica correttamente X_3 non è importante per la previsione della distribuzione di Y. Questo è qualcosa che la misura MDA originale di Random Forests tende a sbagliare, come dimostrato nell’articolo medio. Inoltre, notiamo ancora una volta che i valori mancanti in X non ci sono problemi qui.
Conclusione
GRF/DRF e anche la tradizionale Random Forest non dovrebbero mancare nella cassetta degli attrezzi di qualsiasi data scientist. Sebbene metodi come XGboost possano avere prestazioni migliori nella previsione tradizionale, i numerosi punti di forza dei moderni approcci basati su RF li rendono uno strumento incredibilmente versatile.
Naturalmente, si dovrebbe tenere presente che questi metodi sono ancora completamente non parametrici e sono necessari molti punti dati affinché l’adattamento abbia senso. Ciò è particolarmente vero per la quantificazione dell’incertezza, che è valida solo in modo asintotico, cioè per campioni “grandi”.
Letteratura
(1) Breiman, L. (2001). Foreste casuali. Apprendimento automatico, 45(1):5–32.
Appendice: Codice
require(drf)
require(Matrix)
require(kernlab)drfCI <- function(X, Y, B, sampling = "binomial", ...) {
n <- dim(X)(1)
# compute point estimator and DRF per halfsample
# weightsb: B times n matrix of weights
DRFlist <- lapply(seq_len(B), function(b) {
# half-sample index
indexb <- if (sampling == "binomial") {
seq_len(n)(as.logical(rbinom(n, size = 1, prob = 0.5)))
} else {
sample(seq_len(n), floor(n / 2), replace = FALSE)
}
## Using normal Bootstrap on the data and refitting DRF
DRFb <-
drfown(X = X(indexb, , drop = F), Y = Y(indexb, , drop = F), ...)
return(list(DRF = DRFb, indices = indexb))
})
return(list(DRFlist = DRFlist, X = X, Y = Y))
}
predictdrf <- function(DRF, newdata, functional = NULL, ...) {
##Predict for testpoints in newdata, with B weights for each point, representing
##uncertainty
ntest <- nrow(x)
n <- nrow(DRF$Y)
weightsb <- lapply(DRF$DRFlist, function(l) {
weightsbfinal <- Matrix(0, nrow = ntest, ncol = n, sparse = TRUE)
weightsbfinal(, l$indices) <- predict(l$DRF, x)$weights
return(weightsbfinal)
})
weightsall <- Reduce("+", weightsb) / length(weightsb)
if (!is.null(functional)) {
stopifnot("Not yet implemented for several x" = ntest == 1)
thetahatb <-
lapply(weightsb, function(w)
functional(weights = w, X = DRF$X, Y = DRF$Y, x = x))
thetahatbforvar <- do.call(rbind, thetahatb)
thetahat <- functional(weights = weightsall, X = DRF$X, Y = DRF$Y, x = x)
thetahat <- matrix(thetahat, nrow = dim(x)(1))
var_est <- if (dim(thetahat)(2) > 1) {
a <- sweep(thetahatbforvar, 2, thetahat, FUN = "-")
crossprod(a, a) / B
} else {
mean((c(thetahatbforvar) - c(thetahat)) ^ 2)
}
return(list(weights = weightsall, thetahat = thetahat, weightsb = weightsb,
var_est = var_est))
} else {
return(list(weights = weightsall, weightsb = weightsb))
}
}
drfown <- function(X, Y,
num.trees = 500,
splitting.rule = "FourierMMD",
num.features = 10,
bandwidth = NULL,
response.scaling = TRUE,
node.scaling = FALSE,
sample.weights = NULL,
sample.fraction = 0.5,
mtry = min(ceiling(sqrt(ncol(X)) + 20), ncol(X)),
min.node.size = 15,
honesty = TRUE,
honesty.fraction = 0.5,
honesty.prune.leaves = TRUE,
alpha = 0.05,
imbalance.penalty = 0,
compute.oob.predictions = TRUE,
num.threads = NULL,
seed = stats::runif(1, 0, .Machine$integer.max),
compute.variable.importance = FALSE) {
# initial checks for X and Y
if (is.data.frame(X)) {
if (is.null(names(X))) {
stop("the regressor should be named if provided under data.frame format.")
}
if (any(apply(X, 2, class) %in% c("factor", "character"))) {
any.factor.or.character <- TRUE
X.mat <- as.matrix(fastDummies::dummy_cols(X, remove_selected_columns = TRUE))
} else {
any.factor.or.character <- FALSE
X.mat <- as.matrix(X)
}
mat.col.names.df <- names(X)
mat.col.names <- colnames(X.mat)
} else {
X.mat <- X
mat.col.names <- NULL
mat.col.names.df <- NULL
any.factor.or.character <- FALSE
}
if (is.data.frame(Y)) {
if (any(apply(Y, 2, class) %in% c("factor", "character"))) {
stop("Y should only contain numeric variables.")
}
Y <- as.matrix(Y)
}
if (is.vector(Y)) {
Y <- matrix(Y,ncol=1)
}
#validate_X(X.mat)
if (inherits(X, "Matrix") && !(inherits(X, "dgCMatrix"))) {
stop("Currently only sparse data of class 'dgCMatrix' is supported.")
}
drf:::validate_sample_weights(sample.weights, X.mat)
#Y <- validate_observations(Y, X)
# set legacy GRF parameters
clusters <- vector(mode = "numeric", length = 0)
samples.per.cluster <- 0
equalize.cluster.weights <- FALSE
ci.group.size <- 1
num.threads <- drf:::validate_num_threads(num.threads)
all.tunable.params <- c("sample.fraction", "mtry", "min.node.size", "honesty.fraction",
"honesty.prune.leaves", "alpha", "imbalance.penalty")
# should we scale or not the data
if (response.scaling) {
Y.transformed <- scale(Y)
} else {
Y.transformed <- Y
}
data <- drf:::create_data_matrices(X.mat, outcome = Y.transformed, sample.weights = sample.weights)
# bandwidth using median heuristic by default
if (is.null(bandwidth)) {
bandwidth <- drf:::medianHeuristic(Y.transformed)
}
args <- list(num.trees = num.trees,
clusters = clusters,
samples.per.cluster = samples.per.cluster,
sample.fraction = sample.fraction,
mtry = mtry,
min.node.size = min.node.size,
honesty = honesty,
honesty.fraction = honesty.fraction,
honesty.prune.leaves = honesty.prune.leaves,
alpha = alpha,
imbalance.penalty = imbalance.penalty,
ci.group.size = ci.group.size,
compute.oob.predictions = compute.oob.predictions,
num.threads = num.threads,
seed = seed,
num_features = num.features,
bandwidth = bandwidth,
node_scaling = ifelse(node.scaling, 1, 0))
if (splitting.rule == "CART") {
##forest <- do.call(gini_train, c(data, args))
forest <- drf:::do.call.rcpp(drf:::gini_train, c(data, args))
##forest <- do.call(gini_train, c(data, args))
} else if (splitting.rule == "FourierMMD") {
forest <- drf:::do.call.rcpp(drf:::fourier_train, c(data, args))
} else {
stop("splitting rule not available.")
}
class(forest) <- c("drf")
forest(("ci.group.size")) <- ci.group.size
forest(("X.orig")) <- X.mat
forest(("is.df.X")) <- is.data.frame(X)
forest(("Y.orig")) <- Y
forest(("sample.weights")) <- sample.weights
forest(("clusters")) <- clusters
forest(("equalize.cluster.weights")) <- equalize.cluster.weights
forest(("tunable.params")) <- args(all.tunable.params)
forest(("mat.col.names")) <- mat.col.names
forest(("mat.col.names.df")) <- mat.col.names.df
forest(("any.factor.or.character")) <- any.factor.or.character
if (compute.variable.importance) {
forest(('variable.importance')) <- variableImportance(forest, h = bandwidth)
}
forest
}
#' Variable importance for Distributional Random Forests
#'
#' @param X Matrix with input training data.
#' @param Y Matrix with output training data.
#' @param X_test Matrix with input testing data. If NULL, out-of-bag estimates are used.
#' @param num.trees Number of trees to fit DRF. Default value is 500 trees.
#' @param silent If FALSE, print variable iteration number, otherwise nothing is print. Default is FALSE.
#'
#' @return The list of importance values for all input variables.
#' @export
#'
#' @examples
compute_drf_vimp <- function(X, Y, X_test = NULL, num.trees = 500, silent = FALSE){
# fit initial DRF
bandwidth_Y <- drf:::medianHeuristic(Y)
k_Y <- rbfdot(sigma = bandwidth_Y)
K <- kernelMatrix(k_Y, Y, Y)
DRF <- drfown(X, Y, num.trees = num.trees)
wall <- predict(DRF, X_test)$weights
# compute normalization constant
wbar <- colMeans(wall)
wall_wbar <- sweep(wall, 2, wbar, "-")
I0 <- as.numeric(sum(diag(wall_wbar %*% K %*% t(wall_wbar))))
# compute drf importance dropping variables one by one
I <- sapply(1:ncol(X), function(j) {
if (!silent){print(paste0('Running importance for variable X', j, '...'))}
DRFj <- drfown(X = X(, -j, drop=F), Y = Y, num.trees = num.trees)
DRFpredj <- predict(DRFj, X_test(, -j))
wj <- DRFpredj$weights
Ij <- sum(diag((wj - wall) %*% K %*% t(wj - wall)))/I0
return(Ij)
})
# compute retraining bias
DRF0 <- drfown(X = X, Y = Y, num.trees = num.trees)
DRFpred0 = predict(DRF0, X_test)
w0 <- DRFpred0$weights
vimp0 <- sum(diag((w0 - wall) %*% K %*% t(w0 - wall)))/I0
# compute final importance (remove bias & truncate negative values)
vimp <- sapply(I - vimp0, function(x){max(0,x)})
names(vimp)<-colnames(X)
return(vimp)
}
Fonte: towardsdatascience.com


