Uno dei tipi di dati più popolari è una serie temporale. Video, immagini, pixel, segnali, letteralmente tutto ciò che ha una componente temporale potrebbe essere trasformato in esso. Formalmente, una serie temporale è una sequenza di storico misure di una variabile osservabile a intervalli di tempo uguali.
In questo articolo voglio suggerire una piccola pipeline che chiunque può utilizzare quando analizza una serie temporale. Potrebbe aiutarti a ricavare informazioni significative sui dati stessi, prepararli per la modellazione e trarre alcune conclusioni preliminari.
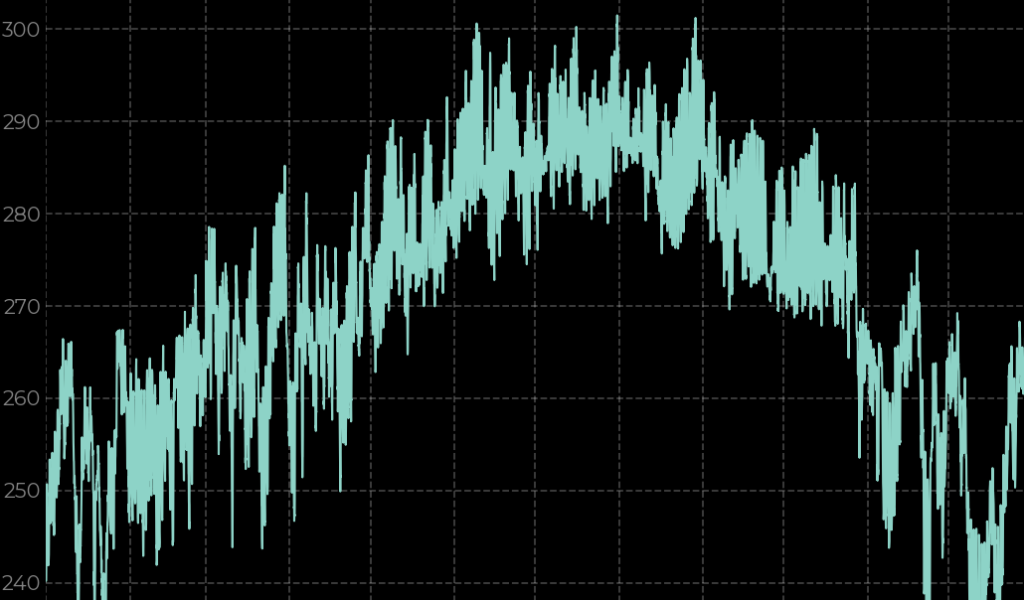
Dato che la mia parola preferita è geospaziale ðŸŒ, oggi analizzeremo una serie temporale meteorologica. In particolare, esploreremo la temperatura dell'aria a 2 m, le precipitazioni totali, la radiazione solare netta superficiale e la pressione superficiale nel punto della Siberia sud-orientale nel corso del 2023, derivati da valori orari ERA5 Terra (1) rianalisi del clima.
Come sempre, per seguire il tutorial, è possibile scaricare ed eseguire il notebook Qui.
Per realizzare l'analisi dobbiamo importare diverse librerie:
import pandas as pd
import seaborn as sns
import numpy as npimport matplotlib.pyplot as plt
import xarray as xr
import statsmodels.api as sm
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from scipy import stats
Ho anche deciso di provare un nuovo stile matplotlib da due librerie, supponente E ambivalente:
from ambivalent import STYLES
import opinionated
plt.style.use(STYLES('ambivalent'))
plt.style.use("dark_background")
Prima di tutto carichiamo e visualizziamo i dati che abbiamo. Per gestire array geospaziali multidimensionali utilizzeremo Bene biblioteca.
data = xr.open_dataset('Medium_data.nc')
data
Ora dobbiamo suddividere i dati in modo specifico per la posizione scelta, convertirli in un dataframe panda e creare un grafico a linee:
df = data.sel(latitude=52.53, longitude=101.63, method='pad').to_pandas().drop(('latitude', 'longitude'), axis=1)
fig, ax = plt.subplots(ncols = 2, nrows = 2, figsize=(16,9))
df('t2m').plot(ax=ax(0,0))
ax(0,0).set_title('Air Temperature')
df('ssr').plot(ax=ax(0,1))
ax(0,1).set_title('Surface Net Solar Radiation')
df('sp').plot(ax=ax(1,0))
ax(1,0).set_title('Surface Pressure')
df('tp').plot(ax=ax(1,1))
ax(1,1).set_title('Total Precipitation')
plt.tight_layout()
plt.show()
È già chiaro dai grafici a linee che tutte e quattro le serie temporali hanno caratteristiche diverse, quindi analizziamole utilizzando strumenti matematici.
Qualsiasi serie temporale ha tre attributi importanti da considerare:
- Tendenzache è un cambiamento graduale a lungo termine in una serie temporale;
- Stagionalitàche si riferisce ad una serie storica con una variazione periodica regolare della media della serie;
- Rumore (residui), che è una componente casuale di un segnale con media pari a zero.
Per ottenere ciascuno di questi componenti separatamente, è possibile produrli decomposizione classica (additivo o moltiplicativo). Questa operazione viene prodotta applicando un filtro convoluzionale, quindi ogni componente della serie temporale viene definito come uno dei due
O
Dove sì – è un valore da una serie temporale, S – componenti stagionali, T – componente di tendenza e N – rumore.
Per produrre la scomposizione, oltre a selezionare il tipo di scomposizione, è necessario impostare un periodo stagionale (es. p=1 per annuale, p=4 per trimestrale, p=12 per mensile ecc.).
È importante ricordare che la suddetta scomposizione classica è un metodo davvero ingenuo e semplice. Presenta limitazioni significative come la sua linearità, l’incapacità di catturare la stagionalità dinamica e la difficoltà nel gestire la non stazionarietà in una serie temporale. Tuttavia, ai fini di questo articolo questo metodo è più che sufficiente.
Per fare la scomposizione classica useremo season_decompose funzione dalla libreria statsmodels con un periodo uguale a 24, poiché abbiamo a che fare con dati orari:
vars = {'t2m': 'Air Temperature', 'tp': 'Total Precipitation', 'sp': 'Surface Pressure', 'ssr': 'Surface Net Solar Radiation'}
for var in df.columns:
result = sm.tsa.seasonal_decompose(df(var), model='additive', period = 24)
results_df = pd.DataFrame({'trend': result.trend, 'seasonal': result.seasonal, 'resid': result.resid, 'observed': result.observed})
fig, ax = plt.subplots(ncols = 2, nrows = 2,figsize=(16,9))
ax(0,0).plot(df.index, results_df.trend)
ax(0,0).set_title('Trend')
ax(0,0).set_ylabel('Value')ax(0,1).plot(df.index, results_df.seasonal)
ax(0,1).set_title('Seasonal')
ax(1,0).plot(df.index, results_df.resid)
ax(1,0).set_title('Residual')
ax(1,0).set_ylabel('Value')
ax(1,0).set_xlabel('time')
ax(1,1).plot(df.index, results_df.observed)
ax(1,1).set_title('Observed')
ax(1,1).set_xlabel('time')
opinionated.set_title_and_suptitle(vars(var), f"Dickey-Fuller test: {round(sm.tsa.stattools.adfuller(df(var))(1),5)}", position_title=(0.45,1),
position_sub_title=(0.95, 1))
plt.tight_layout()
plt.savefig(f'Seasonal_{var}.png')
plt.show()
Puoi vedere che per tutte le variabili la componente stagionale sembra un disastro. Poiché analizziamo i dati orari, queste variazioni stagionali vengono osservate nell'arco di un giorno e non sono realmente informative. In questo caso, vale la pena provare a ricampionare i dati con la risoluzione giornaliera ed eseguire la scomposizione per il periodo di un giorno.
df_d = df.resample('1d').mean()
A questo punto alcuni di voi probabilmente avranno notato l'etichetta del test Dickey-Fuller nell'angolo in alto a destra del grafico. Questo è un stazionarietà test, che è stato eseguito utilizzando il file adfill funzione della stessa libreria. Nel caso di una serie temporale, la stazionarietà significa che le proprietà di una serie temporale non cambiano nel tempo. Quando parlo di proprietà intendo varianza, stagionalità, trend e autocorrelazione.
Quando applichiamo il test Augmented Dickey-Fuller (ADF) a una serie temporale poniamo un'ipotesi nulla che la serie temporale non sia stazionaria. Quindi selezioniamo un livello di significatività α, che di solito è del 5%. In sostanza, α è la probabilità di rifiutare erroneamente l'ipotesi nulla quando in realtà è vera. Quindi nel nostro caso, α=5%, c'è il 5% di rischio di concludere che la serie temporale è stazionaria, quando in realtà non lo è.
Il risultato del test ci fornirà un valore p. Se è inferiore a 0,05, possiamo rifiutare la nostra ipotesi nulla.
Come puoi vedere, tutte e 4 le variabili sono stazionarie secondo il test ADF.
Di solito, per applicare alcuni modelli di previsione delle serie temporali come ARIMA e altri, la stazionarietà è un must, quindi in questo caso siamo fortunati. In generale, i dati meteorologici e climatici vengono spesso analizzati in diversi materiali didattici relativi a serie temporali, poiché nella maggior parte dei casi sono stazionari.
Dopo aver concluso che tutte le nostre serie temporali sono stazionarie, diamo un'occhiata a come sono distribuite. Per fare ciò utilizzeremo la nota libreria Seaborn e la sua funzione trama di coppiache permette di creare grafici informativi con hists e kdes.
ax = sns.pairplot(df, diag_kind='kde')
ax.map_upper(sns.histplot, bins=20)
ax.map_lower(sns.kdeplot, levels=5, color='.1')
plt.show()
Consideriamo l'esempio di t2m (1 riga e 1 colonna). Analizzando il grafico della stima della densità del kernel (kde) è chiaro che la distribuzione di questa variabile è multimodale, nel senso che ha 2 o più “campane”. Quindi durante le fasi successive di questo articolo proveremo a trasformare la variabile per assomigliare a a distribuzione normale.
Altri grafici nella prima colonna e riga sono identici in termini di informazioni che forniscono, ma vengono visualizzati in modo diverso. Fondamentalmente si tratta di grafici a dispersione, che permettono di identificare come due variabili sono correlate. Quindi più scuro è il colore di un punto o più vicino al cerchio centrale, maggiore è la densità dei punti in quest'area.
Poiché abbiamo scoperto che la serie temporale della temperatura dell'aria è stazionaria, ma non distribuita normalmente, proviamo a risolverla utilizzando la trasformazione di Box-Cox. Per fare ciò utilizzeremo il pacchetto scipy e la sua funzione boxcox.
df_d('t2m_box'), _ = stats.boxcox(df_d.t2m)
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(15,7))
sns.histplot(df_d.t2m_box, kde=True, ax=ax(0))
sns.histplot(df_d.t2m, kde=True, ax=ax(1))
La parte sinistra del grafico è la distribuzione delle nostre serie temporali dopo la trasformazione di BoxCox e, come puoi vedere, è ancora lontana dall'essere definita distribuita “normalmente”. Ma se lo confrontiamo con quello a destra, possiamo dire che si è decisamente avvicinato a quello normale.
Un'altra cosa che possiamo fare per assicurarci che la trasformazione eseguita sia stata utile è creare un grafico delle probabilità. In sostanza, tracciamo i quantili di una distribuzione teorica (nel nostro caso normale) rispetto a campioni dei nostri dati empirici (cioè le serie temporali che consideriamo). Più i punti sono vicini alla linea bianca, meglio è.
fig = plt.figure()ax1 = fig.add_subplot(211)
prob = stats.probplot(df_d.t2m, dist=stats.norm, plot=ax1)
ax1.get_lines()(1).set_color('w')
ax1.get_lines()(0).set_color('#8dd3c7')
ax1.set_title('Probplot against normal distribution')
ax2 = fig.add_subplot(212)
prob = stats.probplot(df_d.t2m_box, dist=stats.norm, plot=ax2)
ax2.get_lines()(1).set_color('w')
ax2.get_lines()(0).set_color('#8dd3c7')
ax2.set_title('Probplot after Box-Cox transformation')
plt.tight_layout()fig = plt.figure()
ax1 = fig.add_subplot(211)
prob = stats.probplot(df_d.t2m, dist=stats.norm, plot=ax1)
ax1.set_title('Probplot against normal distribution')
ax2 = fig.add_subplot(212)
prob = stats.probplot(df_d.t2m_box, dist=stats.norm, plot=ax2)
ax2.set_title('Probplot after Box-Cox transformation')
plt.tight_layout()
Se intendi utilizzare le serie temporali trasformate per la modellazione ML, non dimenticare di applicare la trasformazione BoxCox inversa, altrimenti dovrai affrontare numeri inadeguati!
E l'ultimo passaggio della nostra analisi è l'autocorrelazione. La funzione di autocorrelazione (ACF) stima la correlazione tra una serie temporale e una sua versione ritardata. O in altre parole, come un valore specifico di una serie temporale è correlato ad altri valori precedenti in intervalli di tempo diversi.
Potrebbe anche essere utile tracciare la funzione di autocorrelazione parziale (PACF), che è uguale all'autocorrelazione, ma con la rimozione della correlazione a ritardi più brevi. Quindi stima la correlazione tra i valori entro un determinato timestamp, ma controllando l'influenza di altri valori.
for var in df.columns(:-1):
fig, (ax1, ax2) = plt.subplots(2,1,figsize=(10,8))
plot_acf(df_d.t2m, ax = ax1)
plot_pacf(df_d.t2m, ax = ax2)
opinionated.set_title_and_suptitle(vars(var), '',position_title=(0.38,1),
position_sub_title=(0.95, 1))
plt.tight_layout()
plt.show()
Come puoi vedere, c'è un'autocorrelazione parziale molto forte nelle serie temporali della pressione superficiale con un intervallo di 1 giorno. Poi si indebolisce notevolmente e dopo 3 giorni di latenza è quasi assente. Tale analisi potrebbe aiutarti a comprendere meglio la natura dei dati con cui hai a che fare e, quindi, a trarre conclusioni più significative.
Fonte: towardsdatascience.com


