Scopri come una rete neurale con un livello nascosto che utilizza l’attivazione ReLU può rappresentare qualsiasi funzione non lineare continua.
Le funzioni di attivazione svolgono un ruolo fondamentale nelle reti neurali (NN) poiché introducono non linearità e consentono alla rete di apprendere caratteristiche e funzioni più complesse rispetto a una semplice regressione lineare. Una delle funzioni di attivazione più comunemente utilizzate è l’Unità Lineare Rettificata (ReLU), che è stata teoricamente mostrato per consentire alle NN di approssimare un’ampia gamma di funzioni continue, rendendole potenti approssimatori di funzioni.
In questo post studiamo in particolare l’approssimazione delle funzioni Non Lineari Continue (CNL), lo scopo principale dell’utilizzo di una NN su un semplice modello di regressione lineare. Più precisamente, indagheremo 2 sottocategorie di funzioni CNL: funzioni lineari continue a pezzi (CPWL) e curve continue (CC). Mostreremo come questi due tipi di funzioni possono essere rappresentati utilizzando una NN costituita da uno strato nascosto, dati un numero sufficiente di neuroni con attivazione ReLU.
A scopo illustrativo, consideriamo solo input di funzionalità singole, ma l’idea si applica anche a input di funzionalità multiple.
ReLU è una funzione lineare a tratti composta da due parti lineari: una che elimina i valori negativi in cui l’output è zero e una che fornisce una mappatura lineare continua per valori non negativi.
Le funzioni CPWL sono funzioni continue con più porzioni lineari. La pendenza è costante su ogni porzione, poi cambia bruscamente nei punti di transizione aggiungendo nuove funzioni lineari.
In una NN con uno strato nascosto che utilizza l’attivazione ReLU e uno strato di output lineare, le attivazioni vengono aggregate per formare la funzione target CPWL. Ogni unità dello strato nascosto è responsabile di un pezzo lineare. Ad ogni unità, viene aggiunta una nuova funzione ReLU che corrisponde al cambiamento di pendenza per produrre la nuova pendenza (cfr. Fig.2). Poiché questa funzione di attivazione è sempre positiva, i pesi dello strato di output corrispondenti alle unità che aumentano la pendenza saranno positivi e, viceversa, i pesi corrispondenti alle unità che diminuiscono la pendenza saranno negativi (cfr. Fig.3). La nuova funzione viene aggiunta al punto di transizione ma non contribuisce alla funzione risultante prima (e talvolta dopo) quel punto a causa dell’intervallo di disabilitazione della funzione di attivazione ReLU.
Esempio
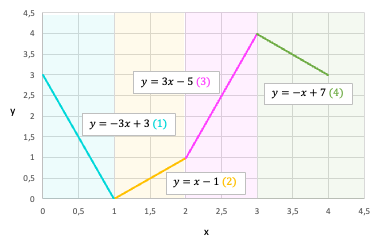
Per renderlo più concreto, consideriamo un esempio di funzione CPWL composta da 4 segmenti lineari definiti come di seguito.
Per rappresentare questa funzione target, utilizzeremo una NN con 1 strato nascosto di 4 unità e uno strato lineare che restituisce la somma ponderata degli output di attivazione dello strato precedente. Determiniamo i parametri della rete in modo che ciascuna unità nello strato nascosto rappresenti un segmento del target. Ai fini di questo esempio, il bias dello strato di output (b2_0) è impostato su 0.
Il prossimo tipo di funzione continua non lineare che studieremo è la funzione CC. Non esiste una definizione corretta per questa sottocategoria, ma un modo informale per definire le funzioni CC sono le funzioni non lineari continue che non sono lineari a tratti. Diversi esempi di funzioni CC sono: funzione quadratica, funzione esponenziale, funzione seno, ecc.
Una funzione CC può essere approssimata da una serie di pezzi lineari infinitesimi, detta approssimazione lineare a tratti della funzione. Maggiore è il numero di pezzi lineari e minore è la dimensione di ciascun segmento, migliore è l’approssimazione alla funzione target. Pertanto, la stessa architettura di rete di prima con un numero sufficientemente elevato di unità nascoste può fornire una buona approssimazione per una funzione curva.
Tuttavia, in realtà, la rete è addestrata per adattarsi a un dato set di dati in cui la funzione di mappatura input-output è sconosciuta. Un’architettura con troppi neuroni è soggetta a overfitting, elevata varianza e richiede più tempo per l’addestramento. Pertanto, un numero appropriato di unità nascoste non deve essere troppo piccolo per adattarsi adeguatamente ai dati, né troppo grande per portare a un overfitting. Inoltre, con un numero limitato di neuroni, una buona approssimazione con bassa perdita ha più punti di transizione in un dominio ristretto, piuttosto che punti di transizione equidistanti in un modo di campionamento uniforme (come mostrato in Fig.10).
In questo post, abbiamo studiato come la funzione di attivazione ReLU consenta a più unità di contribuire alla funzione risultante senza interferire, consentendo così l’approssimazione continua della funzione non lineare. Inoltre, abbiamo discusso della scelta dell’architettura di rete e del numero di unità nascoste per ottenere un buon risultato di approssimazione.
Spero che questo post sia utile per il tuo processo di apprendimento automatico!
Ulteriori domande su cui riflettere:
- Come cambia la capacità di approssimazione se aumenta il numero di layer nascosti con attivazione ReLU?
- Come vengono utilizzate le attivazioni ReLU per un problema di classificazione?
*Se non diversamente specificato, tutte le immagini sono dell’autore
Fonte: towardsdatascience.com


