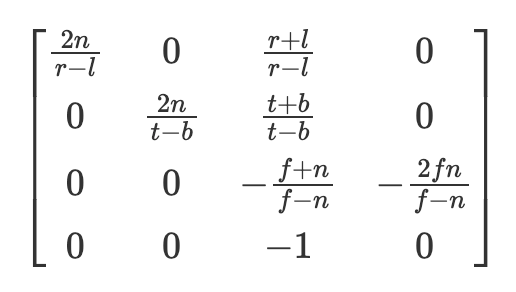
Comprensione e codifica del modo in cui le gaussiane vengono utilizzate all'interno dello splatting gaussiano 3D
Ora passiamo alle gaussiane! La distribuzione preferita da tutti. Se ti sei appena unito a noi, abbiamo spiegato come prendere un punto 3D e tradurlo in 2D data la posizione della telecamera in parte 1. Per questo articolo ci occuperemo della parte gaussiana dello splatting gaussiano. Utilizzeremo part_2.ipynb nel nostro GitHub.
Una piccola modifica che apporteremo qui è che utilizzeremo la proiezione prospettica che utilizza una matrice interna diversa da quella mostrata nell'articolo precedente. Tuttavia, i due sono equivalenti quando si proietta un punto in 2D e trovo che il primo metodo introdotto nella parte 1 sia molto più semplice da capire, tuttavia cambiamo il nostro metodo per replicare, in Python, gran parte del codice dell'autore quanto possibile. Nello specifico, la nostra matrice “interna” sarà ora data dalla matrice di proiezione OpenGL mostrata qui e l'ordine di moltiplicazione sarà ora punti @ external.transpose() @ internal.
Per chi è curioso di conoscere questa nuova matrice interna (altrimenti sentitevi liberi di saltare questo paragrafo) r e l sono i piani di ritaglio dei lati destro e sinistro, essenzialmente quali punti potrebbero essere in vista rispetto alla larghezza della foto, e t e b sono i piani di ritaglio superiore e inferiore. N è il piano di ritaglio vicino (dove verranno proiettati i punti) e f è il piano di ritaglio lontano. Per ulteriori informazioni ho trovato che i capitoli di scratchapixel qui siano piuttosto istruttivi (https://www.scratchapixel.com/lessons/3d-basic-rendering/perspective-and-orthographic-projection-matrix/opengl-perspective-projection-matrix.html). Ciò restituisce anche i punti nelle coordinate del dispositivo normalizzate (tra -1 e 1) e che poi proiettiamo in coordinate pixel. Digressione a parte il compito rimane lo stesso, prendere il punto in 3D e proiettarlo su un piano dell'immagine 2D. Tuttavia, in questa parte del tutorial ora utilizziamo le gaussiane anziché i punti.
def getIntinsicMatrix(
focal_x: torch.Tensor,
focal_y: torch.Tensor,
height: torch.Tensor,
width: torch.Tensor,
znear: torch.Tensor = torch.Tensor((100.0)),
zfar: torch.Tensor = torch.Tensor((0.001)),,
) -> torch.Tensor:
"""
Gets the internal perspective projection matrixznear: near plane set by user
zfar: far plane set by user
fovX: field of view in x, calculated from the focal length
fovY: field of view in y, calculated from the focal length
"""
fovX = torch.Tensor((2 * math.atan(width / (2 * focal_x))))
fovY = torch.Tensor((2 * math.atan(height / (2 * focal_y))))
tanHalfFovY = math.tan((fovY / 2))
tanHalfFovX = math.tan((fovX / 2))
top = tanHalfFovY * znear
bottom = -top
right = tanHalfFovX * znear
left = -right
P = torch.zeros(4, 4)
z_sign = 1.0
P(0, 0) = 2.0 * znear / (right - left)
P(1, 1) = 2.0 * znear / (top - bottom)
P(0, 2) = (right + left) / (right - left)
P(1, 2) = (top + bottom) / (top - bottom)
P(3, 2) = z_sign
P(2, 2) = z_sign * zfar / (zfar - znear)
P(2, 3) = -(zfar * znear) / (zfar - znear)
return P
Uno schema gaussiano 3D è costituito dalle coordinate x, yez e dalla matrice di covarianza associata. Come notato dagli autori: “Un approccio ovvio sarebbe quello di ottimizzare direttamente la matrice di covarianza Σ per ottenere gaussiane 3D che rappresentano il campo di radianza”. Tuttavia, le matrici di covarianza hanno significato fisico solo quando sono semidefinite positive. Per l'ottimizzazione di tutti i nostri parametri, utilizziamo la discesa del gradiente che non può essere facilmente vincolata per produrre matrici valide, mentre i passaggi e i gradienti di aggiornamento possono creare molto facilmente matrici di covarianza non valide.†¹
Pertanto, gli autori utilizzano una scomposizione della matrice di covarianza che produrrà sempre matrici di covarianza semidefinite positive. In particolare utilizzano 3 parametri di “scala” e 4 quaternioni che vengono trasformati in una matrice di rotazione 3×3 (R). La matrice di covarianza è quindi data da
Notare che è necessario normalizzare il vettore quaternione prima di convertirlo in una matrice di rotazione per ottenere una matrice di rotazione valida. Pertanto nella nostra implementazione un punto gaussiano è costituito dai seguenti parametri, coordinate (vettore 3×1), quaternioni (vettore 4×1), scala (vettore 3×1) e un valore float finale relativo all'opacità (quanto è trasparente lo splat). Ora tutto ciò che dobbiamo fare è ottimizzare questi 11 parametri per ottenere la nostra scena: semplice, vero!
Beh, a quanto pare è un po' più complicato di così. Se ricordi la matematica del liceo, la forza di una gaussiana in un punto specifico è data dall'equazione:
Tuttavia, ci preoccupiamo della forza delle gaussiane 3D in 2D, ad es. nel piano dell'immagine. Ma potresti dire che sappiamo come proiettare i punti in 2D! Nonostante ciò, non abbiamo ancora esaminato la proiezione della matrice di covarianza in 2D e quindi non potremmo trovare l'inverso della matrice di covarianza 2D se non abbiamo ancora trovato la matrice di covarianza 2D.
Ora questa è la parte divertente (dipende da come la guardi). EWA Splatting, un articolo di riferimento degli autori di splatting gaussiano 3D, mostra esattamente come proiettare la matrice di covarianza 3D in 2D.² Tuttavia, ciò presuppone la conoscenza di una matrice di trasformazione affine Jacobiana, che calcoliamo di seguito. Trovo che il codice sia molto utile quando si affronta un concetto difficile e quindi ne ho forniti alcuni di seguito per esemplificare come passare da una matrice di covarianza 3D a 2D.
def compute_2d_covariance(
points: torch.Tensor,
external_matrix: torch.Tensor,
covariance_3d: torch.Tensor,
tan_fovY: torch.Tensor,
tan_fovX: torch.Tensor,
focal_x: torch.Tensor,
focal_y: torch.Tensor,
) -> torch.Tensor:
"""
Compute the 2D covariance matrix for each gaussian
"""
points = torch.cat(
(points, torch.ones(points.shape(0), 1, device=points.device)), dim=1
)
points_transformed = (points @ external_matrix)(:, :3)
limx = 1.3 * tan_fovX
limy = 1.3 * tan_fovY
x = points_transformed(:, 0) / points_transformed(:, 2)
y = points_transformed(:, 1) / points_transformed(:, 2)
z = points_transformed(:, 2)
x = torch.clamp(x, -limx, limx) * z
y = torch.clamp(y, -limy, limy) * zJ = torch.zeros((points_transformed.shape(0), 3, 3), device=covariance_3d.device)
J(:, 0, 0) = focal_x / z
J(:, 0, 2) = -(focal_x * x) / (z**2)
J(:, 1, 1) = focal_y / z
J(:, 1, 2) = -(focal_y * y) / (z**2)
# transpose as originally set up for perspective projection
# so we now transform back
W = external_matrix(:3, :3).T
return (J @ W @ covariance_3d @ W.T @ J.transpose(1, 2))(:, :2, :2)
Prima di tutto, tan_fovY e tan_fovX sono le tangenti di metà degli angoli del campo visivo. Usiamo questi valori per bloccare le nostre proiezioni, impedendo che eventuali proiezioni selvagge fuori schermo influenzino il nostro rendering. È possibile derivare lo Jacobiano dalla trasformazione da 3D a 2D come indicato con la nostra trasformazione diretta iniziale introdotta nella parte 1, ma ti ho risparmiato il problema e ho mostrato la derivazione prevista sopra. Infine, se ricordi, abbiamo trasposto la nostra matrice di rotazione sopra per consentire un rimpasto dei termini e quindi trasponiamo nuovamente sulla penultima riga prima di restituire il calcolo della covarianza finale. Come nota lo splatting paper dell'EWA, possiamo ignorare la terza riga e colonna poiché ci interessa solo il piano dell'immagine 2D. Potresti chiederti: perché non abbiamo potuto farlo fin dall'inizio? Bene, i parametri della matrice di covarianza varieranno a seconda dell'angolo da cui la guardi poiché nella maggior parte dei casi non sarà una sfera perfetta! Ora che siamo passati al punto di vista corretto, le informazioni sulla covarianza dell'asse z sono inutili e possono essere scartate.
Dato che abbiamo la matrice di covarianza 2D, siamo vicini a poter calcolare l'impatto che ciascuna gaussiana ha su qualsiasi pixel casuale nella nostra immagine, dobbiamo solo trovare la matrice di covarianza invertita. Ricorda ancora dall'algebra lineare che per trovare l'inversa di una matrice 2×2 devi solo trovare il determinante e poi rimescolare i termini. Ecco del codice che ti aiuterà anche attraverso questo processo.
def compute_inverted_covariance(covariance_2d: torch.Tensor) -> torch.Tensor:
"""
Compute the inverse covariance matrixFor a 2x2 matrix
given as
((a, b),
(c, d))
the determinant is ad - bc
To get the inverse matrix reshuffle the terms like so
and multiply by 1/determinant
((d, -b),
(-c, a)) * (1 / determinant)
"""
determinant = (
covariance_2d(:, 0, 0) * covariance_2d(:, 1, 1)
- covariance_2d(:, 0, 1) * covariance_2d(:, 1, 0)
)
determinant = torch.clamp(determinant, min=1e-3)
inverse_covariance = torch.zeros_like(covariance_2d)
inverse_covariance(:, 0, 0) = covariance_2d(:, 1, 1) / determinant
inverse_covariance(:, 1, 1) = covariance_2d(:, 0, 0) / determinant
inverse_covariance(:, 0, 1) = -covariance_2d(:, 0, 1) / determinant
inverse_covariance(:, 1, 0) = -covariance_2d(:, 1, 0) / determinant
return inverse_covariance
E poi, ora possiamo calcolare la forza dei pixel per ogni singolo pixel in un'immagine. Tuttavia, farlo è estremamente lento e inutile. Ad esempio, non abbiamo davvero bisogno di sprecare potenza di calcolo per capire come uno splat in (0,0) influisce su un pixel in (1000, 1000), a meno che la matrice di covarianza non sia massiccia. Pertanto, gli autori scelgono di calcolare quello che chiamano il “raggio” di ogni simbolo. Come visto nel codice seguente, calcoliamo gli autovalori lungo ciascun asse (ricorda, gli autovalori mostrano la variazione). Quindi, prendiamo la radice quadrata dell'autovalore più grande per ottenere una misura della deviazione standard e la moltiplichiamo per 3,0, che copre il 99,7% della distribuzione entro 3 deviazioni standard. Questo raggio ci aiuta a capire i valori xey minimi e massimi toccati dallo splat. Durante il rendering, calcoliamo solo la forza della splat per i pixel entro questi limiti, risparmiando un sacco di calcoli non necessari. Abbastanza intelligente, vero?
def compute_extent_and_radius(covariance_2d: torch.Tensor):
mid = 0.5 * (covariance_2d(:, 0, 0) + covariance_2d(:, 1, 1))
det = covariance_2d(:, 0, 0) * covariance_2d(:, 1, 1) - covariance_2d(:, 0, 1) ** 2
intermediate_matrix = (mid * mid - det).view(-1, 1)
intermediate_matrix = torch.cat(
(intermediate_matrix, torch.ones_like(intermediate_matrix) * 0.1), dim=1
)max_values = torch.max(intermediate_matrix, dim=1).values
lambda1 = mid + torch.sqrt(max_values)
lambda2 = mid - torch.sqrt(max_values)
# now we have the eigenvalues, we can calculate the max radius
max_radius = torch.ceil(3.0 * torch.sqrt(torch.max(lambda1, lambda2)))
return max_radius
Tutti questi passaggi sopra ci forniscono la nostra scena preelaborata che può quindi essere utilizzata nella nostra fase di rendering. Ricapitolando, ora abbiamo i punti in 2D, i colori associati a tali punti, la covarianza in 2D, la covarianza inversa in 2D, l'ordine di profondità ordinato, i valori minimo x, minimo y, massimo x, massimo y per ogni simbolo e i valori associati opacità. Con tutti questi componenti possiamo finalmente passare al rendering di un'immagine!
Fonte: towardsdatascience.com


