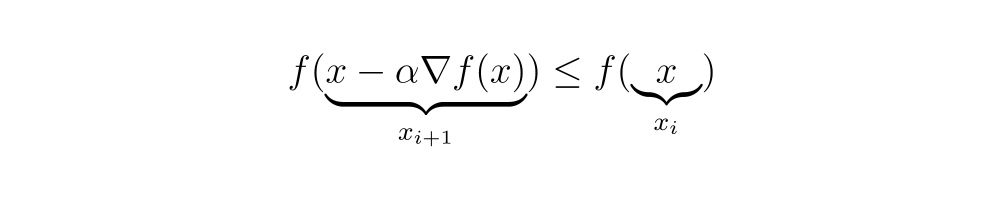
Questo algoritmo è noto come “Gradient Descent” o “Metodo della discesa più ripida”, essendo un metodo di ottimizzazione per trovare il minimo di una funzione in cui ogni passo viene eseguito nella direzione del gradiente negativo. Questo metodo non garantisce che venga trovato il minimo globale della funzione, ma piuttosto un minimo locale.
Le discussioni sulla ricerca del minimo globale potrebbero essere sviluppate in un altro articolo, ma qui abbiamo dimostrato matematicamente come il gradiente può essere utilizzato per questo scopo.
Ora applichiamolo alla funzione di costo E questo dipende da N pesi wabbiamo:
Per aggiornare tutti gli elementi di W in base alla discesa del gradiente abbiamo:
E per qualsiasi N-esimo elemento ð '¤ del vettore Wabbiamo:
Pertanto, abbiamo il nostro algoritmo di apprendimento teorico. Logicamente, questo non si applica all’ipotetica idea del cuoco, ma piuttosto ai numerosi algoritmi di machine learning che conosciamo oggi.
Sulla base di quanto visto possiamo concludere la dimostrazione e la prova matematica dell'algoritmo di apprendimento teorico. Tale struttura viene applicata a numerosi metodi di apprendimento come AdaGrad, Adam e Stochastic Gradient Descent (SGD).
Questo metodo non garantisce di trovare il file N-valori di peso w dove il funzione di costo restituisce un risultato pari a zero o molto vicino ad esso. Tuttavia, ci assicura che verrà trovato un minimo locale della funzione di costo.
Per affrontare il problema dei minimi locali, esistono diversi metodi più robusti, come SGD e Adam, comunemente utilizzati nel deep learning.
Tuttavia, comprendere la struttura e la dimostrazione matematica dell'algoritmo di apprendimento teorico basato sulla discesa del gradiente faciliterà la comprensione di algoritmi più complessi.
Riferimenti
Carreira-Perpinan, MA e Hinton, GE (2005). Sull’apprendimento contrastivo delle divergenze. In RG Cowell e Z. Ghahramani (a cura di), Intelligenza artificiale e statistica, 2005. (pp. 33–41). Fort Lauderdale, FL: Società per l'intelligenza artificiale e la statistica.
García Cabello, J. Reti neurali matematiche. Assiomi 2022, 11, 80.
Geoffrey E. Hinton, Simon Osindero, Yee-Perché Teh. Un algoritmo di apprendimento rapido per reti di credenze profonde. Calcolo neurale 18, 1527–1554. Istituto di Tecnologia del Massachussetts
LeCun, Y., Bottou, L., & Haffner, P. (1998). Apprendimento basato sui gradienti applicato al riconoscimento dei documenti. Atti dell'IEEE, 86(11), 2278–2324.
Fonte: towardsdatascience.com


