Come costruiamo un PINN per l'equazione di Burgers non viscosi con formulazione shock
Reti neurali informate dalla fisica (PIN) sono un tipo speciale di reti neurali. Stimano le soluzioni alle equazioni differenziali parziali incorporando le leggi fisiche che governano un dato set di dati nel processo di apprendimento.
Un esempio di tale equazione è l'equazione di Burgers non viscida, un prototipo di leggi di conservazione che possono sviluppare onde d'urto.
La letteratura attuale fatica ad affrontare efficacemente questo problema. Poiché le onde d'urto non sono soluzioni continue, soddisfano le equazioni solo in senso debole. Modelli temporali continui che dipendono esclusivamente dall’addestramento dei campioni, come il metodo di differenziazione algoritmica, non possono catturare le onde d’urto. Questi metodi sono applicabili solo ai casi di regolarità funzionale.
Si potrebbe tentare di utilizzare Modelli temporali discreti dove le reti neurali e la discretizzazione temporale lavorano insieme per aiutare il modello a formulare shock. Tuttavia, questo metodo diminuisce in qualche modo i vantaggi delle reti neurali informate dalla fisica (PINN) e ritorna ai metodi numerici tradizionali. Questo può essere difficile per qualcuno che capisce le equazioni ma non ha familiarità con le soluzioni numeriche.
In questo articolo affronterò le limitazioni dei modelli temporali continui esistenti dei metodi PINN per l'equazione di Burgers. Introdurrò calcoli per la discontinuità e soluzioni deboli basati sulla differenziazione algoritmica, consentendo all'equazione di catturare gli shock. Questo articolo potrebbe ispirare coloro che sono interessati all'intersezione tra reti neurali e modellizzazione basata sulla fisica, in particolare in ambiti legati alle leggi di conservazione.
Tuttavia, va notato che questo metodo ha mostrato risultati promettenti solo per una delle più semplici equazioni iperboliche unidimensionali. Se possa essere esteso a dimensioni più elevate o ad equazioni più complesse è un aspetto che l'autore non ha esplorato e invito i lettori a contribuire con le proprie idee e risorse su questo argomento.
Secondo l'originale carta: “Le reti neurali informate dalla fisica (PINN) sono addestrate a risolvere compiti di apprendimento supervisionato rispettando le leggi della fisica, descritte da equazioni differenziali alle derivate parziali non lineari generali (PDE). “
Queste PDE assumono in generale la seguente forma (1):
ut + N (u) = 0, x ∈ Ω, t ∈ (0, T),
dove u(t, x) rappresenta la soluzione, N (·) è un operatore differenziale non lineare e Ω è un sottoinsieme dello spazio d-dimensionale.
Indichiamo con
L(u) = ut + N(u).
Si vede subito che f=0 se u è la soluzione dell'equazione. Costruiremo la soluzione u come rete neurale
u = rete_neurale(t,x;pesi)
dove gli input sono le variabili temporali e spaziali. Determiniamo i pesi minimizzando l'errore quadratico medio di f (come detto prima, L(u) dovrebbe essere vicino a 0 se u è la soluzione dell'equazione) e alcune condizioni iniziali e al contorno. Per maggiori dettagli si rimanda al documento originale.
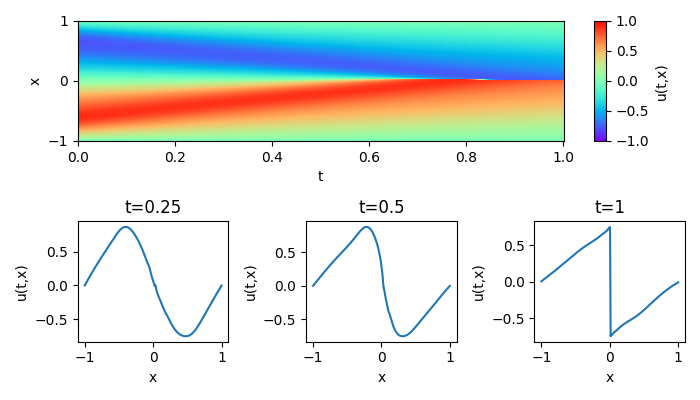
Consideriamo ora l'equazione di Burgers non viscida unidimensionale:
La soluzione dell'equazione, rispettando la condizione iniziale, può essere costruita implicitamente utilizzando il metodo delle caratteristichecioè u=f(x-ut) con la curva caratteristica x
Fonte: towardsdatascience.com
