L'ingenuo Bayes ha spiegato chiaramente con la matematica e scikit-learn | di Yoann Mocquin | Marzo 2024 | Intelligenza-Artificiale

Risolvere il set di dati dell'iride con un approccio gaussiano in scikit-learn.

10 minuti di lettura

·

14 ore fa

In questo post approfondiremo un particolare tipo di classificatore chiamato classificatori naive Bayes. Questi sono metodi che si basano sul teorema di Bayes e sull'ingenuo presupposto che ogni coppia di funzionalità sia condizionatamente indipendente data un'etichetta di classe. Se questo non ha senso per te, continua a leggere!

Come esempio giocattolo, utilizzeremo il noto set di dati dell'iride (Licenza CC BY 4.0) e un tipo specifico di classificatore Bayes ingenuo chiamato classificatore Gaussian Naive Bayes. Ricordare che il set di dati dell'iride è composto da 4 caratteristiche numeriche e il target può essere uno qualsiasi dei 3 tipi di fiore dell'iride (setosa, versicolor, virginica).

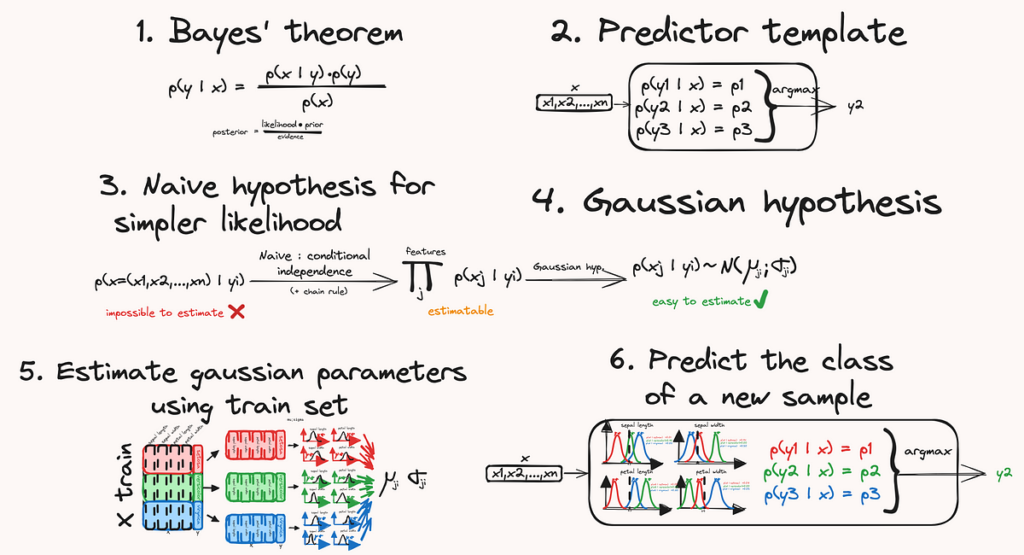
Scomporremo il metodo nei seguenti passaggi:

1. Richiami al teorema di Bayes: questo teorema fornisce la formula matematica che ci permette di stimare la probabilità che un dato campione appartenga a una qualsiasi classe.
2. Possiamo creare un classificatore, uno strumento che restituisce una classe prevista per un campione di input, confrontando la probabilità che questo campione appartenga a una classe, per tutte le classi.
3. Utilizzando la regola della catena e l'ipotesi di indipendenza condizionale, possiamo semplificare la formula della probabilità.
4. Quindi per poter calcolare le probabilità, utilizziamo un'altra ipotesi: che le distribuzioni delle caratteristiche siano gaussiane.
5. Utilizzando un set di addestramento, possiamo stimare i parametri di tali distribuzioni gaussiane.
6. Finalmente disponiamo di tutti gli strumenti necessari per prevedere una classe per un nuovo campione.

Ho molti nuovi post come questo in arrivo; ricordati di iscriverti!

Il teorema di Bayes è un teorema della probabilità che afferma quanto segue:

• P(A|B) è la probabilità condizionata che A sia vera (o che A accada) dato (o sapendo) che B è vera (o B è accaduto) – chiamata anche probabilità a posteriori di A dato B (posteriore: abbiamo aggiornato la probabilità che A è vero dopo che sappiamo che B è vero).