Quantificazione dell'incertezza e perché dovresti preoccuparti | di Jonte Dancker | Aprile 2024 | Intelligenza-Artificiale

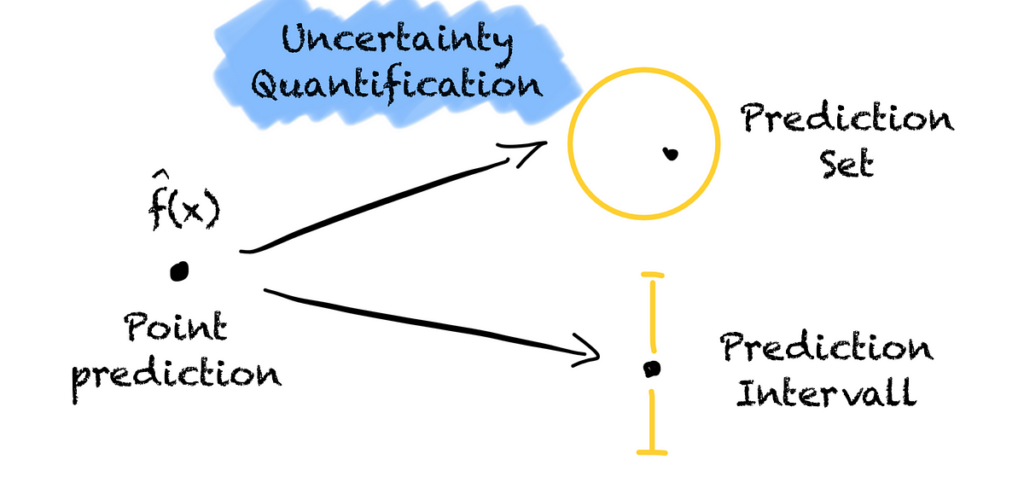
Ora sappiamo perché abbiamo bisogno della quantificazione dell’incertezza per il machine learning e quanto siano utili le regioni di previsione.

Ma come possiamo quantificare l’incertezza di un modello ML?

Supponiamo di lavorare per un'azienda che classifica le immagini di animali per capire quanto spesso appare una determinata specie in una determinata regione. In passato, una persona guardava ogni immagine per identificare l'animale. Questo processo ha richiesto molto tempo. Quindi, costruiamo un modello che classifica l'animale in ciascuna immagine. Per essere utile, il modello deve essere corretto almeno nel 90% dei casi.

Ma il compito è complicato. Il nostro modello di classificazione multiclasse raggiunge solo una precisione dell'85% sul nostro set di test.

Quindi, vogliamo che il modello ci dica quanto è certo riguardo a un'immagine. Se il modello è sicuro che la sua previsione sia corretta con una probabilità superiore al 90%, utilizziamo la classe prevista del modello. Altrimenti, avremo uno sguardo umano sull'immagine.

Ma come possiamo sapere se il modello è certo oppure no? Cominciamo prima con un approccio ingenuo.

Molti modelli di classificazione restituiscono il punteggio di probabilità di ciascuna classe. Prendiamoli e fidiamoci di loro. Ogni volta che il modello classifica un'immagine con una probabilità maggiore di 0,9 ci fidiamo del modello. Se la probabilità è inferiore, diamo l'immagine a un essere umano.

Diamo al modello l'immagine di un cane. Il modello ritiene che si tratti di un cane con una probabilità di 0,95. Il modello sembra essere molto certo. Quindi, ci fidiamo del modello.

Per l'immagine di un gatto, tuttavia, il modello ritiene che l'immagine mostri una giraffa con una probabilità di 0,8. Poiché la probabilità del modello è inferiore al nostro obiettivo del 90% di probabilità, scartiamo l'immagine e la diamo a un essere umano.

Lo facciamo con molte immagini che la modella non ha mai visto prima.

Infine, testiamo la copertura di questo approccio per tutte le immagini che abbiamo classificato. Purtroppo dobbiamo renderci conto che abbiamo una copertura inferiore al nostro obiettivo del 90%. Ci sono troppe previsioni sbagliate.

Cosa abbiamo fatto di sbagliato?

Bene, ci siamo fidati del punteggio di probabilità del modello.

Ma il punteggio non è calibrato e non garantisce la corretta copertura dei nuovi dati. Il punteggio verrebbe calibrato se tutte le classificazioni con un punteggio di 0,9 contenessero la vera classe il 90% delle volte. Ma questo non è il caso del punteggio di “probabilità” dei modelli di classificazione.

Molti approcci presentano lo stesso problema, ad esempio il ridimensionamento di Platt, la regressione isotonica, gli intervalli predittivi bayesiani o il bootstrap. Questi non sono calibrati o si basano su forti ipotesi di distribuzione.

Ma come ottenere una copertura garantita?

Sembra che dobbiamo solo scegliere una soglia migliore.

Quindi, continuiamo a utilizzare il punteggio di “probabilità” del modello. Ma questa volta trasformiamo il punteggio in una misura di incertezza. In questo caso, uno meno il punteggio di “probabilità” del modello per una classe, ovvero 1 — s(x). Quanto più piccolo è il valore, tanto più sicuro è il modello che la sua previsione sia la vera classe.

Per determinare la soglia, utilizziamo i dati che il modello non ha visto durante l'addestramento. Calcoliamo il punteggio di non conformità della vera classe per ciascun campione del set. Quindi ordiniamo questi punteggi da basso (il modello è certo) ad alto (il modello è incerto).

Si noti che in questa fase calcoliamo solo il punteggio di non conformità per la classe reale. Non ci interessa se il modello fosse giusto o sbagliato.

Usiamo la distribuzione risultante per calcolare la soglia q_hat dove il 90% dei punteggi sono inferiori. Il nostro 90esimo percentile della distribuzione. Un punteggio inferiore a questa soglia coprirà la classe reale con una probabilità del 90%.

Ora, ogni volta che facciamo una nuova previsione, calcoliamo il punteggio di non conformità per tutte le classi. Quindi inseriamo tutte le classi con un punteggio inferiore alla soglia nel nostro set di previsioni. Questo è tutto.

Con questo possiamo garantire che la vera classe sarà nella previsione impostata con una probabilità del 90%.

Per la nostra classificazione degli animali, ci fidiamo di tutte le previsioni che contengono un solo animale nel set di previsioni. Se l'insieme di previsioni contiene più di una classe, lasciamo che una persona controlli la nostra classificazione.