Squilibrio di classe: esplorazione delle tecniche di sottocampionamento | di Essam Wisam | Ottobre 2023 | Intelligenza-Artificiale

Impariamo a conoscere il sottocampionamento e come aiuta a risolvere lo squilibrio di classe

Lo abbiamo spiegato formalmente prima l’effetto dello squilibrio di classe e le sue cause e abbiamo anche spiegato diverse tecniche di sovracampionamento che risolvono questo problema come il sovracampionamento casuale, ROSE, RWO, SMOTE, BorderlineSMOTE1, SMOTE-NC e SMOTE-N. In questa storia, tenteremo di fare un tour simile sulle tecniche di sottocampionamento, partendo dal presupposto che sia ovvio come il sottocampionamento aiuterebbe a risolvere il problema dello squilibrio, data la nostra spiegazione precedente.

Le tecniche di sottocampionamento generalmente rientrano in due categorie principali: controllate e non controllate. Nelle tecniche controllate, l’algoritmo riceve un numero che indica quanti campioni dovrebbero esserci nel set di dati finale; nel frattempo, nelle tecniche non controllate il sottocampionamento viene solitamente eseguito semplicemente rimuovendo i punti che soddisfano alcune condizioni. Non è noto a priori quanti punti soddisferanno tale condizione e ovviamente non può essere controllato. In questa storia, tratteremo due tecniche di sottocampionamento controllato (sottocampionamento casuale e k-mean) e due tecniche di sottocampionamento non controllato (Tomek Links e Edited Nearest Neighbors).

Sottocampionamento casuale ingenuo

In questa tecnica, se così è N_k i punti dovrebbero essere rimossi dalla lezione KPoi N_k i punti vengono scelti casualmente da quella classe per la cancellazione.

Di seguito viene mostrato un esempio di sottocampionamento delle due classi di maggioranza nei dati con tre classi 0, 1 e 2.

Quella che segue è un’animazione che mostra l’output a diversi gradi di sottocampionamento

Notate come questo sia un processo del tutto casuale; non viene fatta alcuna scelta specifica riguardo a quali punti mantenere. La distribuzione dei dati potrebbe essere gravemente alterata a causa di ciò.

K-significa sottocampionamento

Possiamo preservare la distribuzione dei dati prestando più attenzione a quali punti rimuovere (o mantenere). In K-significa sottocampionamento, se è necessario averlo N_k punti per la classe k, viene eseguita la K-media K=N_k portando a N_k centroidi finali. K-significa sottocampionamento, facciamo in modo che quei centri (o il vicino più prossimo di ciascuno di essi; questo è un iperparametro) siano l’ultimo N_k punti per tornare. Poiché i centri stessi preservano la distribuzione dei dati, ciò si traduce in un insieme più piccolo di punti che preservano anche i dati.

Di seguito viene mostrato un esempio di sottocampionamento delle due classi di maggioranza nei dati con tre classi 0, 1 e 2.

Si noti come sia più attento in termini di preservazione della struttura dei dati rispetto al sottocampionamento casuale che sarebbe ancora più evidente con un sottocampionamento maggiore. Lo illustriamo ulteriormente con un’animazione:

Si noti che i centri dipendono dall’inizializzazione che in genere implica casualità.

Sottocampionamento dei collegamenti Tomek

Si tratta di una tecnica di sottocampionamento incontrollato in cui un punto può essere rimosso se fa parte di un collegamento Tomek. Due punti formano un collegamento Tomek se:

• Appartengono a classi diverse
• Ciascuno dei due punti è il vicino più prossimo dell’altro punto

La logica qui è che tali punti non aiutano a migliorare il confine decisionale (ad esempio, possono rendere più semplice l’overfitting) e che forse creano rumore. Di seguito è riportato un esempio di applicazione di Tomek Links:

Si noti come dopo il sottocampionamento sia più facile trovare un limite decisionale più lineare, oltre a ciò porta anche i dati a un migliore equilibrio. In questo caso, abbiamo saltato il sottocampionamento della classe minoritaria in verde e abbiamo smesso di sottocampionare per una classe una volta che aveva raggiunto lo stesso numero di punti.

Per vederlo in azione più da vicino, dove tutte le classi alla fine sono sottocampionate, considera la seguente animazione:

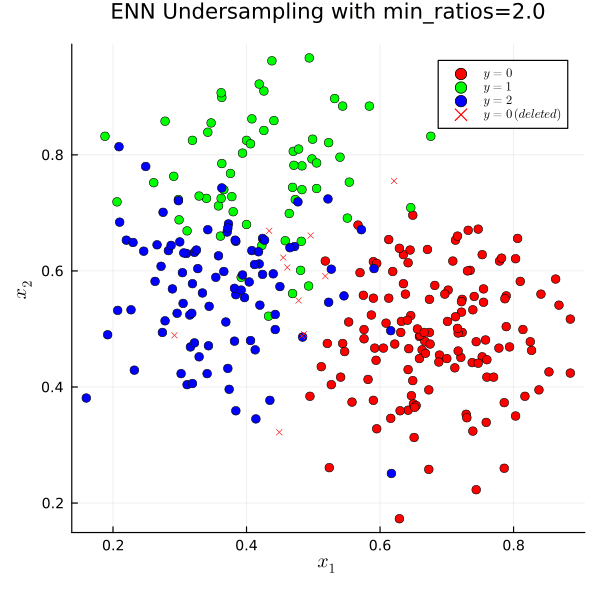
Modificato il sottocampionamento dei vicini più vicini

Sebbene i collegamenti Tomek siano per lo più punti che non aiutano a formare un confine decisionale migliore o che siano rumore, non tutti i punti rumorosi formeranno collegamenti Tomek. Se un punto rumoroso dalla classe k_1 esiste in una regione densa in classe k_2 allora può essere normale che il vicino più vicino al punto rumoroso abbia un punto più vicino che non sia il punto rumoroso, il che implica che rimarrà per non formare un collegamento Tomek. Invece di questa condizione, il sottocampionamento dei vicini più vicini modificato per impostazione predefinita mantiene un punto se e solo se la maggior parte dei vicini appartiene alla stessa classe. C’è anche l’opzione di mantenerli solo se appartengono tutti alla stessa classe o, per un sottocampionamento minimo, di mantenere qualsiasi punto se esista un vicino della stessa classe.

Questa animazione ritrae l’algoritmo in azione:

Notare come elimina più punti che non sarebbero utili per il confine decisionale o che costituiscono rumore. Si può fare ancora più pulizia se il numero di vicini k o la condizione di mantenimento vengono alterati nel modo giusto. Questa è un’altra animazione che illustra l’effetto.

La differenza tra le condizioni “modalità” e “solo modalità” è che la prima mantiene un punto se e solo se la sua classe è una delle più comuni tra i vicini; nel frattempo, quest’ultima mantiene un punto se e solo se la sua classe è l’unica classe più comune.

Questo conclude il nostro tour su alcuni interessanti algoritmi di sottocampionamento. Spero che questo ti abbia aiutato a saperne di più sul sottocampionamento controllato e incontrollato. Alla prossima, arrivederci.

Riferimenti:

(1) Wei-Chao, L., Chih-Fong, T., Ya-Han, H. e Jing-Shang, J. (2017). Sottocampionamento basato sul clustering in dati sbilanciati in classi. Scienze dell’informazione, 409–410, 17–26.

(2) Ivan Tomek. Due modifiche della cnn. IEEE Trans. Sistemi, uomo e cibernetica, 6: 769–772, 1976.

(3) Dennis L. Wilson. Proprietà asintotiche delle regole del vicino più vicino che utilizzano dati modificati. Transazioni IEEE su sistemi, uomo e cibernetica, pagine 408–421, 1972.