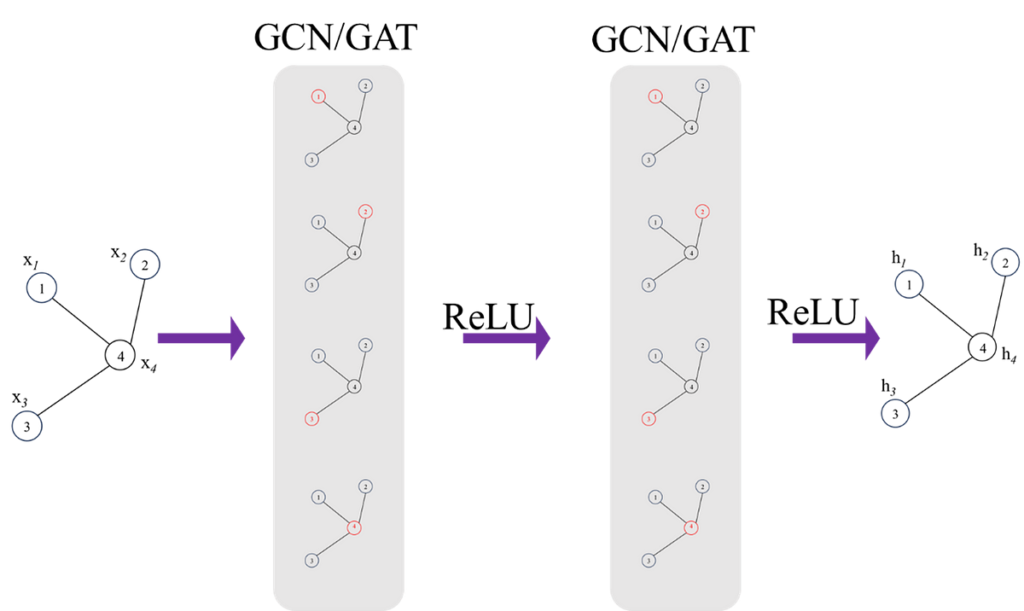
Implementiamo un esempio di regressione in cui l'obiettivo è addestrare una rete a prevedere il valore di un nodo dato il valore di tutti gli altri nodi, ovvero ogni nodo ha una singola caratteristica (che è un valore scalare). Lo scopo di questo esempio è sfruttare le informazioni relazionali intrinseche codificate nel grafico per prevedere con precisione i valori numerici per ciascun nodo. La cosa fondamentale da notare è che inseriamo il valore numerico per tutti i nodi tranne il nodo di destinazione (mascheriamo il valore del nodo di destinazione con 0), quindi prevediamo il valore del nodo di destinazione. Per ciascun punto dati, ripetiamo il processo per tutti i nodi. Forse questo potrebbe sembrare un compito bizzarro, ma vediamo se possiamo prevedere il valore atteso di qualsiasi nodo dati i valori degli altri nodi. I dati utilizzati sono i dati di simulazione corrispondenti a una serie di sensori dell'industria e la struttura grafica che ho scelto nell'esempio seguente si basa sulla struttura effettiva del processo. Ho fornito commenti nel codice per renderlo facile da seguire. È possibile trovare una copia del set di dati Qui (Nota: questi sono i miei dati, generati da simulazioni).
Questo codice e questa procedura di addestramento sono lungi dall'essere ottimizzati, ma il loro scopo è quello di illustrare l'implementazione delle GNN e ottenere un'intuizione su come funzionano. Un problema con il modo in cui ho fatto attualmente che sicuramente non dovrebbe essere fatto in questo modo al di là degli scopi di apprendimento è il mascheramento del valore della caratteristica del nodo e la sua previsione dalla caratteristica dei vicini. Attualmente dovresti eseguire il loop su ciascun nodo (non molto efficiente), un modo molto migliore per farlo è impedire al modello di includere le proprie funzionalità nella fase di aggregazione e quindi non avresti bisogno di fare un nodo alla volta ma ho pensato che fosse più semplice creare un'intuizione per il modello con il metodo attuale 🙂
Preelaborazione dei dati
Importazione delle librerie necessarie e dei dati del sensore dal file CSV. Normalizza tutti i dati nell'intervallo da 0 a 1.
import pandas as pd
import torch
from torch_geometric.data import Data, Batch
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.model_selection import train_test_split
import numpy as np
from torch_geometric.data import DataLoader# load and scale the dataset
df = pd.read_csv('SensorDataSynthetic.csv').dropna()
scaler = MinMaxScaler()
df_scaled = pd.DataFrame(scaler.fit_transform(df), columns=df.columns)
Definire la connettività (indice dei bordi) tra i nodi nel grafico utilizzando un tensore PyTorch, ovvero questo fornisce la topologia grafica del sistema.
nodes_order = (
'Sensor1', 'Sensor2', 'Sensor3', 'Sensor4',
'Sensor5', 'Sensor6', 'Sensor7', 'Sensor8'
)# define the graph connectivity for the data
edges = torch.tensor((
(0, 1, 2, 2, 3, 3, 6, 2), # source nodes
(1, 2, 3, 4, 5, 6, 2, 7) # target nodes
), dtype=torch.long)
I dati importati da CSV hanno una struttura tabellare ma per utilizzarla nelle GNN è necessario trasformarla in una struttura grafica. Ogni riga di dati (un'osservazione) è rappresentata come un grafico. Scorri ogni riga per creare una rappresentazione grafica dei dati
Viene creata una maschera per ciascun nodo/sensore per indicare la presenza (1) o l'assenza (0) di dati, consentendo flessibilità nella gestione dei dati mancanti. Nella maggior parte dei sistemi potrebbero esserci elementi senza dati disponibili, da qui la necessità di flessibilità nella gestione dei dati mancanti. Suddividere i dati in set di training e test
graphs = ()# iterate through each row of data to create a graph for each observation
# some nodes will not have any data, not the case here but created a mask to allow us to deal with any nodes that do not have data available
for _, row in df_scaled.iterrows():
node_features = ()
node_data_mask = ()
for node in nodes_order:
if node in df_scaled.columns:
node_features.append((row(node)))
node_data_mask.append(1) # mask value of to indicate present of data
else:
# missing nodes feature if necessary
node_features.append(2)
node_data_mask.append(0) # data not present
node_features_tensor = torch.tensor(node_features, dtype=torch.float)
node_data_mask_tensor = torch.tensor(node_data_mask, dtype=torch.float)
# Create a Data object for this row/graph
graph_data = Data(x=node_features_tensor, edge_index=edges.t().contiguous(), mask = node_data_mask_tensor)
graphs.append(graph_data)
#### splitting the data into train, test observation
# Split indices
observation_indices = df_scaled.index.tolist()
train_indices, test_indices = train_test_split(observation_indices, test_size=0.05, random_state=42)
# Create training and testing graphs
train_graphs = (graphs(i) for i in train_indices)
test_graphs = (graphs(i) for i in test_indices)
Visualizzazione del grafico
La struttura del grafico creata sopra utilizzando gli indici dei bordi può essere visualizzata utilizzando networkx.
import networkx as nx
import matplotlib.pyplot as pltG = nx.Graph()
for src, dst in edges.t().numpy():
G.add_edge(nodes_order(src), nodes_order(dst))
plt.figure(figsize=(10, 8))
pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=True, node_color='lightblue', edge_color='gray', node_size=2000, font_weight='bold')
plt.title('Graph Visualization')
plt.show()
Definizione del modello
Definiamo il modello. Il modello incorpora 2 strati convoluzionali GAT. Il primo livello trasforma le caratteristiche del nodo in uno spazio a 8 dimensioni e il secondo livello GAT lo riduce ulteriormente a una rappresentazione a 8 dimensioni.
I GNN sono altamente suscettibili all'overfitting, la regolazione (dropout) viene applicata dopo ogni strato GAT con una probabilità definita dall'utente per evitare l'overfitting. Lo strato di dropout azzera essenzialmente in modo casuale alcuni degli elementi del tensore di input durante l'addestramento.
I risultati di output del livello di convoluzione GAT vengono passati attraverso un livello (lineare) completamente connesso per mappare l'output a 8 dimensioni sulla caratteristica del nodo finale che in questo caso è un valore scalare per nodo.
Mascherare il valore del Nodo target; come accennato in precedenza, lo scopo di questo compito è regredire il valore del nodo target in base al valore dei suoi vicini. Questo è il motivo per mascherare/sostituire il valore del nodo di destinazione con zero.
from torch_geometric.nn import GATConv
import torch.nn.functional as F
import torch.nn as nnclass GNNModel(nn.Module):
def __init__(self, num_node_features):
super(GNNModel, self).__init__()
self.conv1 = GATConv(num_node_features, 16)
self.conv2 = GATConv(16, 8)
self.fc = nn.Linear(8, 1) # Outputting a single value per node
def forward(self, data, target_node_idx=None):
x, edge_index = data.x, data.edge_index
edge_index = edge_index.T
x = x.clone()
# Mask the target node's feature with a value of zero!
# Aim is to predict this value from the features of the neighbours
if target_node_idx is not None:
x(target_node_idx) = torch.zeros_like(x(target_node_idx))
x = F.relu(self.conv1(x, edge_index))
x = F.dropout(x, p=0.05, training=self.training)
x = F.relu(self.conv2(x, edge_index))
x = F.relu(self.conv3(x, edge_index))
x = F.dropout(x, p=0.05, training=self.training)
x = self.fc(x)
return x
Addestrare il modello
Inizializzazione del modello e definizione dell'ottimizzatore, della funzione di perdita e degli iperparametri tra cui tasso di apprendimento, decadimento del peso (per la regolarizzazione), batch_size e numero di epoche.
model = GNNModel(num_node_features=1)
batch_size = 8
optimizer = torch.optim.Adam(model.parameters(), lr=0.0002, weight_decay=1e-6)
criterion = torch.nn.MSELoss()
num_epochs = 200
train_loader = DataLoader(train_graphs, batch_size=1, shuffle=True)
model.train()
Il processo di addestramento è abbastanza standard, ogni grafico (un punto dati) di dati viene passato attraverso il passaggio in avanti del modello (iterando su ciascun nodo e prevedendo il nodo di destinazione. La perdita derivante dalla previsione viene accumulata sulla dimensione batch definita prima dell'aggiornamento la GNN attraverso la backpropagation.
for epoch in range(num_epochs):
accumulated_loss = 0
optimizer.zero_grad()
loss = 0
for batch_idx, data in enumerate(train_loader):
mask = data.mask
for i in range(1,data.num_nodes):
if mask(i) == 1: # Only train on nodes with data
output = model(data, i) # get predictions with the target node masked
# check the feed forward part of the model
target = data.x(i)
prediction = output(i).view(1)
loss += criterion(prediction, target)
#Update parameters at the end of each set of batches
if (batch_idx+1) % batch_size == 0 or (batch_idx +1 ) == len(train_loader):
loss.backward()
optimizer.step()
optimizer.zero_grad()
accumulated_loss += loss.item()
loss = 0average_loss = accumulated_loss / len(train_loader)
print(f'Epoch {epoch+1}, Average Loss: {average_loss}')
Testare il modello addestrato
Utilizzando il set di dati di test, passa ciascun grafico attraverso il passaggio in avanti del modello addestrato e prevedi il valore di ciascun nodo in base al valore dei suoi vicini.
test_loader = DataLoader(test_graphs, batch_size=1, shuffle=True)
model.eval()actual = ()
pred = ()
for data in test_loader:
mask = data.mask
for i in range(1,data.num_nodes):
output = model(data, i)
prediction = output(i).view(1)
target = data.x(i)
actual.append(target)
pred.append(prediction)
Visualizzazione dei risultati del test
Usando iplot possiamo visualizzare i valori previsti dei nodi rispetto ai valori di verità fondamentali.
import plotly.graph_objects as go
from plotly.offline import iplotactual_values_float = (value.item() for value in actual)
pred_values_float = (value.item() for value in pred)
scatter_trace = go.Scatter(
x=actual_values_float,
y=pred_values_float,
mode='markers',
marker=dict(
size=10,
opacity=0.5,
color='rgba(255,255,255,0)',
line=dict(
width=2,
color='rgba(152, 0, 0, .8)',
)
),
name='Actual vs Predicted'
)
line_trace = go.Scatter(
x=(min(actual_values_float), max(actual_values_float)),
y=(min(actual_values_float), max(actual_values_float)),
mode='lines',
marker=dict(color='blue'),
name='Perfect Prediction'
)
data = (scatter_trace, line_trace)
layout = dict(
title='Actual vs Predicted Values',
xaxis=dict(title='Actual Values'),
yaxis=dict(title='Predicted Values'),
autosize=False,
width=800,
height=600
)
fig = dict(data=data, layout=layout)
iplot(fig)
Nonostante la mancanza di messa a punto dell'architettura del modello o degli iperparametri, in realtà ha svolto un lavoro decente, potremmo mettere a punto ulteriormente il modello per ottenere una maggiore precisione.
Questo ci porta alla fine di questo articolo. Le GNN sono relativamente più nuove rispetto ad altri rami dell'apprendimento automatico, sarà molto emozionante vedere gli sviluppi di questo campo ma anche la sua applicazione a diversi problemi. Infine, grazie per aver dedicato del tempo a leggere questo articolo, spero che tu lo abbia trovato utile per comprendere le GNN o il loro background matematico.
Se non diversamente specificato, tutte le immagini sono dell'autore
Fonte: towardsdatascience.com


