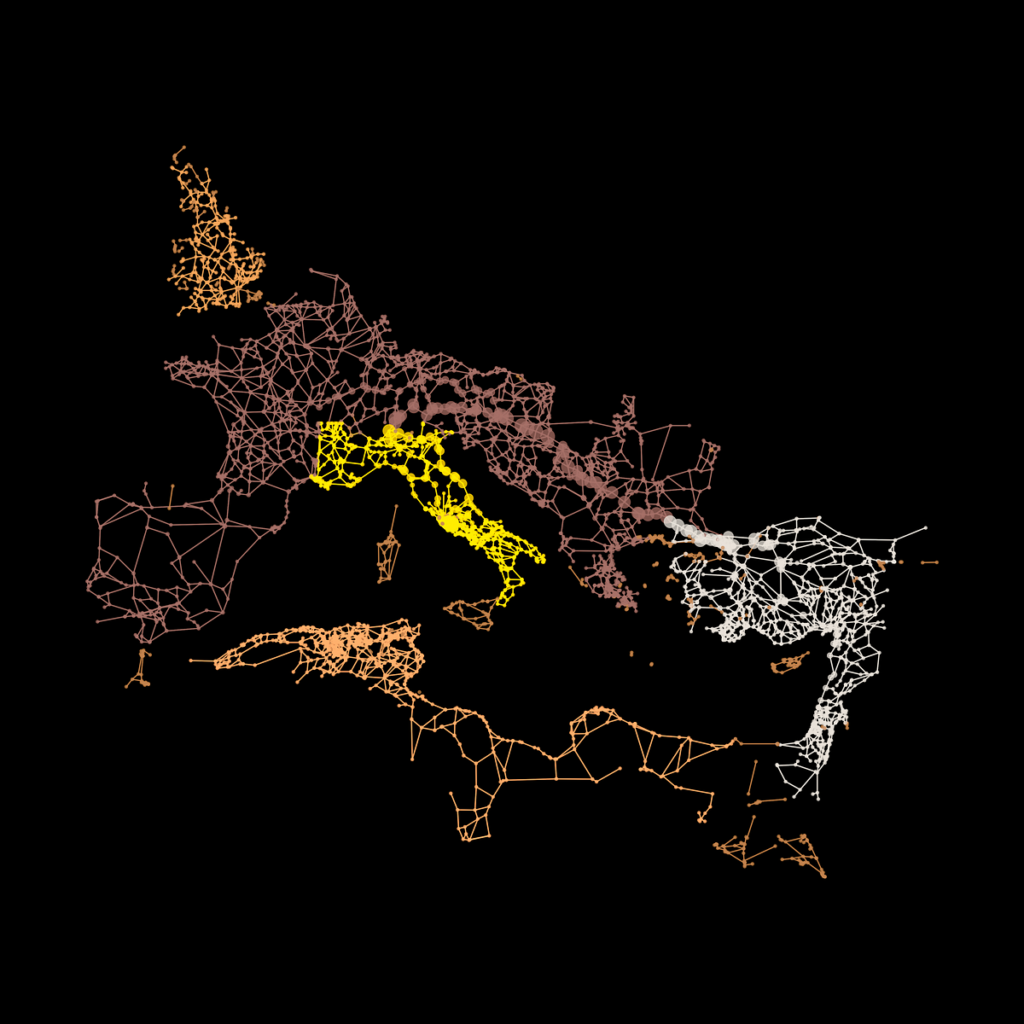
Dopo aver apprezzato le immagini, torniamo al grafico stesso e quantifichiamolo. Qui, calcolerò il grado totale di ciascun nodo, misurando il numero di connessioni che ha, e la centralità di betweenness non normalizzata di ciascun nodo, contando il numero totale di percorsi più brevi che attraversano ciascun nodo.
node_degrees = dict(G_clean2.degree)
node_betweenness = dict(nx.betweenness_centrality(G_clean2, normalized = False))
Ora ho i punteggi di importanza di ogni incrocio. Inoltre, nel nodi tabella, abbiamo anche la loro posizione: ora è il momento di passare alla domanda principale. Per questo quantifico l’importanza di ciascun nodo che rientra nei confini amministrativi di Roma. Per questo, avrò bisogno dei confini amministrativi di Roma, che sono relativamente facili da ottenere da OSMnx (nota: la Roma di oggi è probabilmente diversa dalla Roma del passato, ma approssimativamente dovrebbe andare bene).
admin = ox.geocode_to_gdf('Rome, Italy')
admin.plot()
L’output di questa cella:
Inoltre, dal punto di vista visivo, è abbastanza chiaro che Roma non esiste come un unico nodo nella rete stradale; invece, molti sono nelle vicinanze. Abbiamo quindi bisogno di una sorta di binning, di indicizzazione spaziale, che ci aiuti a raggruppare tutti i nodi e le intersezioni della rete stradale appartenenti a Roma. Inoltre, si vorrebbe che questa aggregazione fosse paragonabile in tutto l’Impero. Questo è il motivo per cui, invece di mappare semplicemente i nodi nell’area amministrativa di Roma, sceglierò quello di Uber H3 raggruppamento esagonale e creare griglie esagonali. Quindi, mappa ciascun nodo nell’esagono che lo racchiude e calcola l’importanza aggregata di quell’esagono in base ai punteggi di centralità dei nodi della rete racchiusi. Infine, discuterò di come gli esagoni più centrali si sovrappongono a Roma.
Per prima cosa, otteniamo in modo approssimativo l’area amministrativa dell’Impero Romano:
import alphashape # version: 1.1.0
from descartes import PolygonPatch# take a random sample of the node points
sample = nodes.sample(1000)
sample.plot()
# create its concave hull
points = ((point.x, point.y) for point in sample.geometry)
alpha = 0.95 * alphashape.optimizealpha(points)
hull = alphashape.alphashape(points, alpha)
hull_pts = hull.exterior.coords.xy
fig, ax = plt.subplots()
ax.scatter(hull_pts(0), hull_pts(1), color='red')
ax.add_patch(PolygonPatch(hull, fill=False, color='green'))
L’output di questa cella:
Dividiamo il poligono dell’Impero in una griglia esagonale:
import h3 # version: 3.7.3
from shapely.geometry import Polygon # version: 1.7.1
import numpy as np # version: 1.22.4def split_admin_boundary_to_hexagons(polygon, resolution):
coords = list(polygon.exterior.coords)
admin_geojson = {"type": "Polygon", "coordinates": (coords)}
hexagons = h3.polyfill(admin_geojson, resolution, geo_json_conformant=True)
hexagon_geometries = {hex_id : Polygon(h3.h3_to_geo_boundary(hex_id, geo_json=True)) for hex_id in hexagons}
return gpd.GeoDataFrame(hexagon_geometries.items(), columns = ('hex_id', 'geometry'))
roman_empire = split_admin_boundary_to_hexagons(hull, 3)
roman_empire.plot()
Risultato:
Ora, mappa i nodi della rete stradale in esagoni e collega i punteggi di centralità a ciascun esagono. Poi. Aggrego l’importanza di ciascun nodo all’interno di ciascun esagono sommando il numero di connessioni e il numero di percorsi più brevi che li attraversano:
gdf_merged = gpd.sjoin(roman_empire, nodes(('geometry')))
gdf_merged('degree') = gdf_merged.index_right.map(node_degrees)
gdf_merged('betweenness') = gdf_merged.index_right.map(node_betweenness)
gdf_merged = gdf_merged.groupby(by = 'hex_id')(('degree', 'betweenness')).sum()
gdf_merged.head(3)
Infine, combina i punteggi di centralità aggregati con la mappa esagonale dell’Impero:
roman_empire = roman_empire.merge(gdf_merged, left_on = 'hex_id', right_index = True, how = 'outer')
roman_empire = roman_empire.fillna(0)
E visualizzalo. In questa immagine aggiungo anche la griglia vuota come mappa di base e quindi colore ciascuna cella della griglia in base all’importanza totale dei nodi della rete stradale al suo interno. In questo modo la colorazione evidenzierà in verde le cellule più critiche. Inoltre, ho aggiunto il poligono di Roma in bianco. Innanzitutto, colorato per grado:
f, ax = plt.subplots(1,1,figsize=(15,15))gpd.GeoDataFrame((hull), columns = ('geometry')).plot(ax=ax, color = 'grey', edgecolor = 'k', linewidth = 3, alpha = 0.1)
roman_empire.plot(column = 'degree', cmap = 'RdYlGn', ax = ax)
gdf.plot(ax=ax, color = 'k', linewidth = 0.5, alpha = 0.5)
admin.plot(ax=ax, color = 'w', linewidth = 3, edgecolor = 'w')
ax.axis('off')
plt.savefig('degree.png', dpi = 200)
Risultato:
Fonte: towardsdatascience.com


