Come combinare interessanti proprietà del calcolo quantistico con una classica tecnica di Machine Learning
Sebbene i computer quantistici non siano ancora accessibili a tutti, il Quantum Machine Learning (QML) è un campo di studio promettente poiché utilizza la natura probabilistica intrinseca dei sistemi quantistici per sviluppare modelli. In questo momento, i data scientist di tutto il mondo stanno cercando di capire come sfruttare il paradigma quantistico per produrre modelli migliori e scalabili. Non è possibile quantificare quando ciò avverrà perché dipende anche dall’evoluzione dell’hardware quantistico, ma in questa materia c’è una crescita accelerata.
Nei miei ultimi studi stavo cercando di progettare classificatori quantistici variazionali (VQC), come puoi vedere in un messaggio precedente Scrissi. Questo è un caso di studio interessante se stai iniziando a studiare QML come me.
Tuttavia, ultimamente ho anche iniziato a studiare un approccio quantistico alla Support Vector Machine (SVM) e sono rimasto incuriosito da come l’SVM potesse essere tradotto nel mondo quantistico.
Mentre studiavo i VQC, ero molto parziale e cercavo di indovinare come l’SVM potesse essere tradotto in un circuito quantistico parametrizzabile, ma ho scoperto che il miglioramento quantistico qui funziona in modo diverso, il che è stata una bella sorpresa e mi ha aiutato ad aprire le mie conoscenze mente su questo argomento.
In questo post inizio con una breve introduzione di SVM seguita da come eseguire un approccio QML (Quantum Machine Learning) a questa tecnica e concludo con un esempio di SVM potenziato quantistico (QSVM) utilizzando il set di dati del Titanic.
Presento qui l’SVM focalizzato sui problemi di classificazione, ovvero il Support Vector Classifier (SVC). L’obiettivo di SVC è trovare un iperpiano che separi i dati di diverse classi con il miglior margine possibile. All’inizio non sembra molto utile, vero?
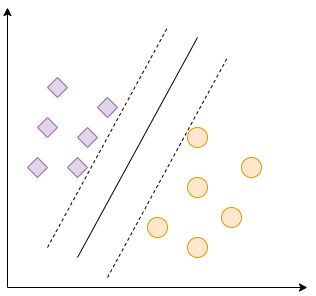
Ma cos’è questo iperpiano che separa le classi? Supponiamo di lavorare con dati in uno spazio vettoriale bidimensionale e di avere due classi, come nella Figura 1.
In questo esempio abbiamo punti dati di 2 classi diverse e possiamo facilmente tracciare una linea che li separa entrambi. La nostra linea continua è l’iperpiano che separa i nostri dati con il miglior margine possibile, come si vede dalle linee tratteggiate. Pertanto, SVM cerca di trovare il miglior separatore.
Potresti pensare che il mio esempio sia troppo ingenuo e che una linea sia un caso molto particolare di iperpiano, il che è un punto valido. Cosa succederebbe se i nostri dati bidimensionali assomigliassero alla Figura 2?
In questo caso non possiamo tracciare una linea che separi correttamente i nostri dati. Se guardiamo questa figura, potremmo disegnare un cerchio come buon separatore. Tuttavia, questa forma non è né una linea né un piano, quindi SVM non è in grado di risolvere direttamente questo problema. Tuttavia, questo è il trucco SVM più interessante e la parte in cui si verifica un iperpiano ad alta dimensione!
E se avessimo la trasformazione di questi dati in uno spazio vettoriale di dimensione superiore? COME:
Quindi potremmo disegnare un aereo:
Che separa le due classi in modo ottimale, come mostrato nella Figura 3:
Nel nostro caso, la funzione f è ciò che chiamiamo kernel, che proietta i dati in uno spazio dimensionale superiore, il che rende più facile trovare un iperpiano in grado di identificare correttamente i dati di classi diverse.
Questa è stata una breve introduzione su kernel e SVM, se sei interessato a maggiori spiegazioni su SVM ti consiglio di leggere questi due post (1 E 2), che rappresentano un’ottima introduzione a SVM e li ho usati entrambi come riferimenti in questo post.
Potresti pensare ora che il mio esempio sia stato molto comodo per spiegare il concetto di kernel, ma come troviamo nella vita reale un kernel adatto che risolva i nostri problemi? Esistono alcuni kernel che sono molto flessibili e sono molto utili per risolvere un buon numero di problemi, come la Radial Basis Function (RBF), che è l’opzione predefinita dell’SVC di scikit-learn. Se sei interessato a saperne di più su questo kernel, lo consiglio questo post. Un dettaglio importante sui kernel come RBF è che non sono descritti da una funzione analitica, ma come una matrice di somiglianza tra punti dati basati sul kernel.
Tuttavia, cosa succede se vogliamo essere più creativi? Se hai letto i miei post precedenti potresti ricordare che una delle proprietà più interessanti dell’informatica quantistica è la relazione esponenziale tra qubit e stati quantistici. Pertanto, un sistema quantistico è un candidato molto interessante per un buon kernel, poiché tende a guidare il nostro sistema verso uno spazio vettoriale ad alta dimensione, a seconda della quantità di qubit che stiamo utilizzando.
I nuclei quantistici sono solitamente definiti da una matrice di similarità basata su un circuito quantistico, che può essere parametrizzabile o meno. Sia Pennylane che Qiskit hanno funzioni integrate che creano kernel che possono essere utilizzati nell’SVC di scikit-learn.
Il progetto di un kernel quantistico prevede alcuni passaggi:
Incorporamento dei dati negli stati quantistici
Progettare un circuito quantistico che possa essere parametrizzabile o meno
In questa fase, è altamente raccomandato lavorare con un certo grado di sovrapposizione ed entanglement tra stati per ottenere il meglio che l’informatica quantistica può offrire.
Costruzione della matrice di similarità
Qui lavoriamo con l’unità unitaria U(|x>) che abbiamo costruito nell’ultimo passaggio e il suo aggiunto per progettare una matrice di similarità.
Qui stiamo progettando un semplice kernel quantistico con Pennylane per utilizzarlo con un SVC di scikit-learn per il set di dati di classificazione del Titanic, dove vogliamo prevedere se una persona è sopravvissuta alla tragedia del Titanic in base a variabili quali età, sesso e classe di imbarco.
Nel nostro esempio utilizziamo le seguenti variabili:
- is_child: se l’età della persona è inferiore a 12 anni (booleano)
- Pclass_1: se la persona è salita nella prima classe (booleano)
- Pclass_2: se la persona è salita nella seconda classe (booleano)
- Sex_female: se il genere della persona è femminile (booleano)
Come puoi vedere, questo è un modello molto semplice con quattro variabili booleane. Stiamo incorporando i nostri dati in stati quantistici utilizzando l’incorporamento quantistico (Basis Embedding), applicando porte Hadamard per applicare la sovrapposizione nei nostri qubit e porte CNOT per generare entanglement.
Questo è un ansatz semplice e non parametrizzabile, ma genera sovrapposizione ed entanglement tra le nostre variabili.
Il codice per creare il kernel e SVM è qui:
import pennylane as qml
from pennylane import numpy as npfrom sklearn.model_selection import train_test_split
import pandas as pd
from sklearn.metrics import accuracy_score
from sklearn.metrics import f1_score, precision_score, recall_score
from sklearn.svm import SVC
num_qubits = 4
def layer(x):
qml.BasisEmbedding(x, wires=range(num_qubits))
for j, wire in enumerate(wires):
qml.Hadamard(wires=(wire))
if j != num_qubits-1:
qml.CNOT(wires=(j, j+1))
else:
qml.CNOT(wires=(j, 0))
def ansatz(x, wires):
layer(x)
adjoint_ansatz = qml.adjoint(ansatz)
dev = qml.device("default.qubit", wires=num_qubits, shots=None)
wires = dev.wires.tolist()
@qml.qnode(dev, interface="autograd")
def kernel_circuit(x1, x2):
ansatz(x1, wires=wires)
adjoint_ansatz(x2, wires=wires)
return qml.probs(wires=wires)
def kernel(x1, x2):
return kernel_circuit(x1, x2)(0)
df_train = pd.read_csv('train.csv')
df_train('Pclass') = df_train('Pclass').astype(str)
df_train = pd.concat((df_train, pd.get_dummies(df_train(('Pclass', 'Sex', 'Embarked')))), axis=1)
X_train, X_test, y_train, y_test = train_test_split(df_train.drop(columns=('Survived')), df_train('Survived'), test_size=0.10, random_state=42, stratify=df_train('Survived'))
X_train('Age') = X_train('Age').fillna(X_train('Age').median())
X_test('Age') = X_test('Age').fillna(X_test('Age').median())
X_train('is_child') = X_train('Age').map(lambda x: 1 if x < 12 else 0)
X_test('is_child') = X_test('Age').map(lambda x: 1 if x < 12 else 0)
cols_model = ('is_child', 'Pclass_1', 'Pclass_2', 'Sex_female')
X_train = X_train(cols_model)
X_test = X_test(cols_model)
X_train = np.array(X_train.values, requires_grad=False)
init_kernel = lambda x1, x2: kernel(x1, x2)
K = qml.kernels.square_kernel_matrix(X_train, init_kernel, assume_normalized_kernel=True)
svm = SVC(kernel=lambda X1, X2: qml.kernels.kernel_matrix(X1, X2, init_kernel)).fit(X_train, y_train)
X_test = np.array(X_test.values, requires_grad=False)
predictions = svm.predict(X_test)
accuracy_score(y_test, predictions)
precision_score(y_test, predictions)
recall_score(y_test, predictions)
f1_score(y_test, predictions, average='macro')
svm1 = SVC(gamma='auto', kernel='rbf')
svm1.fit(X_train, y_train)
y_pred = svm1.predict(X_test)
accuracy_score(y_test, y_pred)
precision_score(y_test, y_pred)
recall_score(y_test, y_pred)
f1_score(y_test, y_pred, average='macro')
I risultati sono:
Come puoi vedere, l’SVC con il kernel RBF ha sovraperformato il nostro SVC con il kernel quantistico. Il nostro approccio quantistico aveva una buona precisione, il che significa che siamo riusciti a evitare falsi positivi a un buon ritmo, ma il nostro ricordo non era così buono, il che implica che abbiamo ottenuto un numero significativo di falsi negativi.
Se vuoi saperne di più sulle SVM con kernel quantistico, questi post sono buoni riferimenti: 1, 2 e questi testi di Pennylane sull’argomento: 3 E 4.
I kernel quantistici possono essere un potente strumento per aumentare le prestazioni SVM. Tuttavia, come abbiamo potuto vedere nel nostro esempio, una SVM con un semplice kernel quantistico non è in grado di sovraperformare una SVM con un kernel RBF. I kernel quantistici richiedono un’attenta progettazione per essere competitivi con le tecniche classiche.
Sto approfondendo i miei studi per progettare kernel quantistici parametrizzabili e spero di avere presto buone notizie su questo argomento.
Fonte: towardsdatascience.com


