Questo articolo fornisce un'introduzione pratica al potenziale dei grafici causali.
Si rivolge a chiunque voglia capirne di più su:
- Cosa sono i grafici causali e come funzionano
- Un caso di studio elaborato in Python che illustra come costruire grafici causali
- Come si confrontano con ML
- Le principali sfide e considerazioni future
Il quaderno completo lo trovate qui:
I grafici causali ci aiutano a distinguere le cause dalle correlazioni. Costituiscono una parte fondamentale degli strumenti di inferenza causale/ML causale/intelligenza artificiale causale e possono essere utilizzati per rispondere a domande causali.
Spesso definito DAG (grafo aciclico diretto), un grafo causale contiene nodi e spigoli: gli spigoli collegano i nodi che sono causalmente correlati.
Esistono due modi per determinare un grafico causale:
- Conoscenza del dominio esperto
- Algoritmi di scoperta causale
Per ora, supponiamo di avere una conoscenza approfondita del dominio per determinare il grafo causale (parleremo degli algoritmi di scoperta causale più avanti).
L'obiettivo del ML è classificare o prevedere nel modo più accurato possibile dati alcuni dati di addestramento. Non vi è alcun incentivo per un algoritmo ML a garantire che le funzionalità che utilizza siano causalmente collegate all’obiettivo. Non vi è alcuna garanzia che la direzione (effetto positivo/negativo) e la forza di ciascuna funzionalità siano allineati al vero processo di generazione dei dati. ML non prenderà in considerazione le seguenti situazioni:
- Correlazioni spurie: due variabili che hanno una correlazione spuria quando hanno una causa comune, ad esempio le alte temperature che aumentano il numero di vendite di gelati e gli attacchi di squali.
- Confondenti: una variabile influenza il trattamento e il risultato, ad esempio la domanda che influisce su quanto spendiamo in marketing e su quanti nuovi clienti si iscrivono.
- Collider: una variabile influenzata da due variabili indipendenti, ad es. Qualità dell'assistenza clienti -> Soddisfazione dell'utente <- Dimensioni dell'azienda
- Mediatori: due variabili collegate (indirettamente) tramite un mediatore, ad esempio esercizio fisico regolare -> idoneità cardiovascolare (il mediatore) -> salute generale
A causa di queste complessità e della natura “scatola nera” del machine learning, non possiamo essere sicuri della sua capacità di rispondere a domande causali.
Dato un grafico causale noto e dati osservati, possiamo addestrare un modello causale strutturale (SCM). Un SCM può essere pensato come una serie di modelli causali, uno per nodo. Ogni modello utilizza un nodo come destinazione e i suoi genitori diretti come funzionalità. Se le relazioni nei nostri dati osservati sono lineari, un SCM sarà una serie di equazioni lineari. Questo potrebbe essere modellato da una serie di modelli di regressione lineare. Se le relazioni nei nostri dati osservati non sono lineari, ciò potrebbe essere modellato con una serie di alberi potenziati.
La differenza fondamentale rispetto al machine learning tradizionale è che un SCM modella le relazioni causali e tiene conto di correlazioni spurie, fattori confondenti, collisori e mediatori.
È comune utilizzare un modello di rumore additivo (ANM) per ciascun nodo non radice (il che significa che ha almeno un genitore). Ciò ci consente di utilizzare una serie di algoritmi di apprendimento automatico (più un termine rumore) per stimare ciascun nodo non radice.
Y := f(X) + N
I nodi radice possono essere modellati utilizzando un modello stocastico per descrivere la distribuzione.
Un SCM può essere visto come un modello generativo in grado di generare nuovi campioni di dati: ciò gli consente di rispondere a una serie di domande causali. Genera nuovi dati campionando dai nodi radice e quindi propagando i dati attraverso il grafico.
Il valore di un SCM è che ci consente di rispondere a domande causali calcolando controfattuali e simulando interventi:
- Controfattuali: utilizzo di dati osservati storicamente per calcolare cosa sarebbe successo a y se avessimo cambiato xeg Cosa sarebbe successo al numero di clienti che abbandonano se avessimo ridotto il tempo di attesa delle chiamate del 20% il mese scorso?
- Interventi: molto simili ai controfattuali (e spesso usati in modo intercambiabile), ma gli interventi simulano cosa accadrebbe in futuro, ad esempio cosa accadrà al numero di clienti che abbandonano se riduciamo il tempo di attesa delle chiamate del 20% l'anno prossimo?
Esistono diversi KPI monitorati dal team del servizio clienti. Uno di questi sono i tempi di attesa delle chiamate. Aumentando il numero del personale del call center diminuiranno i tempi di attesa delle chiamate.
Ma in che modo la riduzione dei tempi di attesa delle chiamate influirà sui livelli di abbandono dei clienti? E questo compenserà il costo del personale aggiuntivo del call center?
Al team di Data Science viene chiesto di costruire e valutare il business case.
La popolazione di interesse è costituita dai clienti che effettuano una chiamata in entrata. Giornalmente vengono raccolti i seguenti dati di serie temporali:
In questo esempio utilizziamo dati di serie temporali, ma i grafici causali possono funzionare anche con dati a livello di cliente.
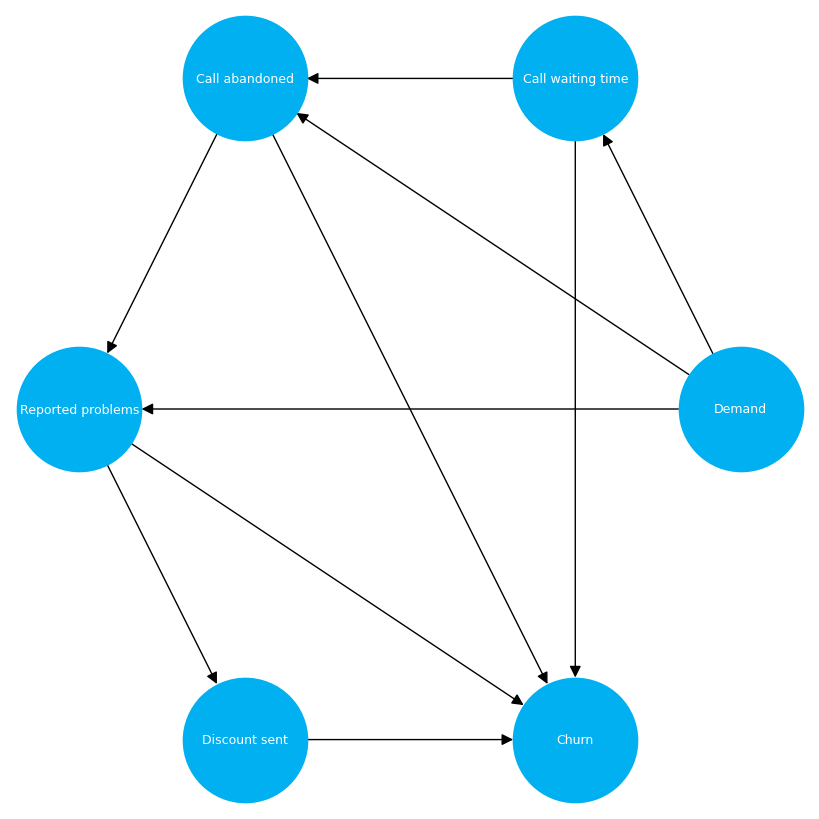
In questo esempio, utilizziamo la conoscenza del dominio esperto per determinare il grafico causale.
# Create node lookup for channels
node_lookup = {0: 'Demand',
1: 'Call waiting time',
2: 'Call abandoned',
3: 'Reported problems',
4: 'Discount sent',
5: 'Churn'
}total_nodes = len(node_lookup)
# Create adjacency matrix - this is the base for our graph
graph_actual = np.zeros((total_nodes, total_nodes))
# Create graph using expert domain knowledge
graph_actual(0, 1) = 1.0 # Demand -> Call waiting time
graph_actual(0, 2) = 1.0 # Demand -> Call abandoned
graph_actual(0, 3) = 1.0 # Demand -> Reported problems
graph_actual(1, 2) = 1.0 # Call waiting time -> Call abandoned
graph_actual(1, 5) = 1.0 # Call waiting time -> Churn
graph_actual(2, 3) = 1.0 # Call abandoned -> Reported problems
graph_actual(2, 5) = 1.0 # Call abandoned -> Churn
graph_actual(3, 4) = 1.0 # Reported problems -> Discount sent
graph_actual(3, 5) = 1.0 # Reported problems -> Churn
graph_actual(4, 5) = 1.0 # Discount sent -> Churn
Successivamente, dobbiamo generare dati per il nostro caso di studio.
Vogliamo generare alcuni dati che ci consentiranno di confrontare il calcolo dei controfattuali utilizzando grafici causali rispetto a ML (per semplificare le cose, regressione di cresta).
Poiché abbiamo identificato il grafico causale nell'ultima sezione, possiamo utilizzare questa conoscenza per creare un processo di generazione di dati.
def data_generator(max_call_waiting, inbound_calls, call_reduction):
'''
A data generating function that has the flexibility to reduce the value of node 0 (Call waiting time) - this enables us to calculate ground truth counterfactualsArgs:
max_call_waiting (int): Maximum call waiting time in seconds
inbound_calls (int): Total number of inbound calls (observations in data)
call_reduction (float): Reduction to apply to call waiting time
Returns:
DataFrame: Generated data
'''
df = pd.DataFrame(columns=node_lookup.values())
df(node_lookup(0)) = np.random.randint(low=10, high=max_call_waiting, size=(inbound_calls)) # Demand
df(node_lookup(1)) = (df(node_lookup(0)) * 0.5) * (call_reduction) + np.random.normal(loc=0, scale=40, size=inbound_calls) # Call waiting time
df(node_lookup(2)) = (df(node_lookup(1)) * 0.5) + (df(node_lookup(0)) * 0.2) + np.random.normal(loc=0, scale=30, size=inbound_calls) # Call abandoned
df(node_lookup(3)) = (df(node_lookup(2)) * 0.6) + (df(node_lookup(0)) * 0.3) + np.random.normal(loc=0, scale=20, size=inbound_calls) # Reported problems
df(node_lookup(4)) = (df(node_lookup(3)) * 0.7) + np.random.normal(loc=0, scale=10, size=inbound_calls) # Discount sent
df(node_lookup(5)) = (0.10 * df(node_lookup(1)) ) + (0.30 * df(node_lookup(2))) + (0.15 * df(node_lookup(3))) + (-0.20 * df(node_lookup(4))) # Churn
return df
# Generate data
np.random.seed(999)
df = data_generator(max_call_waiting=600, inbound_calls=10000, call_reduction=1.00)sns.pairplot(df)
Ora abbiamo una matrice di adiacenza che rappresenta il nostro grafico causale e alcuni dati. Usiamo il modulo gcm dal pacchetto dowhy Python per addestrare un SCM.
È importante pensare a quale meccanismo causale utilizzare per i nodi root e non root. Se guardi la nostra funzione di generatore di dati, vedrai che tutte le relazioni sono lineari. Pertanto la scelta della regressione della cresta dovrebbe essere sufficiente.
# Setup graph
graph = nx.from_numpy_array(graph_actual, create_using=nx.DiGraph)
graph = nx.relabel_nodes(graph, node_lookup)# Create SCM
causal_model = gcm.InvertibleStructuralCausalModel(graph)
causal_model.set_causal_mechanism('Demand', gcm.EmpiricalDistribution()) # Root node
causal_model.set_causal_mechanism('Call waiting time', gcm.AdditiveNoiseModel(gcm.ml.create_ridge_regressor())) # Non-root node
causal_model.set_causal_mechanism('Call abandoned', gcm.AdditiveNoiseModel(gcm.ml.create_ridge_regressor())) # Non-root node
causal_model.set_causal_mechanism('Reported problems', gcm.AdditiveNoiseModel(gcm.ml.create_ridge_regressor())) # Non-root node
causal_model.set_causal_mechanism('Discount sent', gcm.AdditiveNoiseModel(gcm.ml.create_ridge_regressor())) # Non-root
causal_model.set_causal_mechanism('Churn', gcm.AdditiveNoiseModel(gcm.ml.create_ridge_regressor())) # Non-root
gcm.fit(causal_model, df)
È inoltre possibile utilizzare la funzione di assegnazione automatica per assegnare automaticamente i meccanismi causali invece di assegnarli manualmente.
Per maggiori informazioni sul pacchetto gcm vedere la documentazione:
Utilizziamo anche la regressione della cresta per creare un confronto di base. Possiamo guardare indietro al generatore di dati e vedere che stima correttamente i coefficienti per ciascuna variabile. Tuttavia, oltre a influenzare direttamente il tasso di abbandono, il tempo di attesa della chiamata influenza indirettamente il tasso di abbandono attraverso le chiamate abbandonate, i problemi segnalati e gli sconti inviati.
Quando si tratta di stimare i controfattuali, sarà interessante vedere come l’SCM si confronta con la regressione della cresta.
# Ridge regression
y = df('Churn').copy()
X = df.iloc(:, 1:-1).copy()
model = RidgeCV()
model = model.fit(X, y)
y_pred = model.predict(X)print(f'Intercept: {model.intercept_}')
print(f'Coefficient: {model.coef_}')
# Ground truth(0.10 0.30 0.15 -0.20)
Prima di passare al calcolo dei controfattuali utilizzando i grafici causali e la regressione di cresta, abbiamo bisogno di un punto di riferimento della verità concreta. Possiamo utilizzare il nostro generatore di dati per creare campioni controfattuali dopo aver ridotto il tempo di attesa delle chiamate del 20%.
Non potremmo farlo con problemi del mondo reale, ma questo metodo ci consente di valutare quanto siano efficaci il grafico causale e la regressione della cresta.
# Set call reduction to 20%
reduce = 0.20
call_reduction = 1 - reduce# Generate counterfactual data
np.random.seed(999)
df_cf = data_generator(max_call_waiting=600, inbound_calls=10000, call_reduction=call_reduction)
Ora possiamo stimare cosa sarebbe successo se avessimo ridotto il tempo di attesa della chiamata del 20% utilizzando i nostri 3 metodi:
- Verità fondamentale (dal generatore di dati)
- Regressione della cresta
- Grafico causale
Vediamo che la regressione della cresta sottostima significativamente l'impatto sull'abbandono, mentre il grafico causale è molto vicino alla verità fondamentale.
# Ground truth counterfactual
ground_truth = round((df('Churn').sum() - df_cf('Churn').sum()) / df('Churn').sum(), 2)# Causal graph counterfactual
df_counterfactual = gcm.counterfactual_samples(causal_model, {'Call waiting time': lambda x: x*call_reduction}, observed_data=df)
causal_graph = round((df('Churn').sum() - df_counterfactual('Churn').sum()) / (df('Churn').sum()), 3)
# Ridge regression counterfactual
ridge_regression = round((df('Call waiting time').sum() * 1.0 * model.coef_(0) - (df('Call waiting time').sum() * call_reduction * model.coef_(0))) / (df('Churn').sum()), 3)
Questo è stato un semplice esempio per iniziare a pensare al potere dei grafici causali.
Per situazioni più complesse, diverse sfide che avrebbero bisogno di una certa considerazione:
- Quali presupposti vengono fatti e qual è l’impatto della loro violazione?
- E se non avessimo la conoscenza del dominio esperto per identificare il grafo causale?
- Cosa succede se ci sono relazioni non lineari?
- Quanto è dannosa la multi-collinearità?
- Cosa succede se alcune variabili hanno effetti ritardati?
- Come possiamo gestire set di dati ad alta dimensione (molte variabili)?
Tutti questi punti saranno trattati nei blog futuri.
Se sei interessato a saperne di più sull'intelligenza artificiale causale, ti consiglio vivamente le seguenti risorse:
“Incontra Ryan, un esperto lead data scientist con un focus specializzato sull'impiego di tecniche causali in contesti aziendali, che spaziano dal marketing, alle operazioni e al servizio clienti. La sua competenza sta nel svelare le complessità delle relazioni di causa-effetto per guidare un processo decisionale informato e miglioramenti strategici attraverso diverse funzioni organizzative.
Fonte: towardsdatascience.com


