Valutazione di serie storiche sintetiche | di Alexander Nikitin | Dicembre 2023 | Intelligenza-Artificiale

Esplorazione di vari parametri per la valutazione di serie temporali sintetiche con esempi pratici di codice

Questo post del blog è disponibile come file taccuino jupyter su GitHub e fa parte di TSGM, una libreria per la modellazione generativa di serie temporali.

Oggi discuteremo della valutazione di set di dati di serie temporali sintetiche, set di dati creati artificialmente per rappresentare dati reali. Diciamo che esiste un set di dati sintetico D* che mira a rappresentare un set di dati reale D. È essenziale valutare quantitativamente quanto sono buoni questi dati sintetici: D* rappresenta bene D? Questi dati sono sicuri? Questi dati sono preziosi per i problemi a valle? In questo tutorial esamineremo i metodi utilizzati per valutare quantitativamente e qualitativamente la qualità dei dati delle serie temporali sintetiche.

Innanzitutto, consideriamo due casi da (1) che descrivono possibili usi dei dati sintetici:

Scenario 1. Un’organizzazione desidera impiegare un agente esterno per analizzare dati sensibili o studiare metodi statistici per un determinato problema. La condivisione di dati reali può essere complicata a causa della privacy o di problemi commerciali. Le controparti sintetiche possono fornire una soluzione conveniente a questo problema.

Scenario 2. Un’organizzazione desidera addestrare un modello su un set di dati relativamente piccolo. Tuttavia, il set di dati non è sufficiente per la qualità di modellazione desiderata. Tali set di dati limitati possono essere aumentati con dati sintetici. Questi dati sintetici, che devono essere simili ai dati reali, mirano a migliorare le prestazioni del modello o, in altri casi, ad assistere nei test di affidabilità del modello.

Nel complesso, indichiamo e descriviamo in questo tutorial le seguenti metriche:

1. somiglianza reale dei dati (Sc. 1 e 2),

• metrica della distanza,
• metrica discriminativa,
• Punteggio massimo di discrepanza media

2. coerenza predittiva (Sc. 1),

3. efficacia a valle (Sc. 2),

4. privacy (Sc. 1),

5. diversità (Sc. 1 e Sc. 2),

6. Equità (Sc.1 e Sc.2),

7. Confronto visivo (Sc. 1 e 2).

In TSGM, tutte le metriche sono organizzate in modo ordinato tsgm.metrics. Immergiti nei dettagli con la nostra documentazione completa.

Ora diamo il via agli esempi di codifica installando tsgm:

pip install tsgm

Generazione di dati sintetici. Andando avanti, importiamo tsgm e carichiamo un set di dati esemplare. Un tensore Xr ora conterrà 100 serie temporali sinusoidali o costanti (in base alla classe di destinazione yr). Noi useremo (Xr, yr) come un vero (= storico = originale) set di dati. Xs contiene dati sintetici generati da un codificatore automatico variazionale. (Nota: utilizziamo solo un’epoca per la dimostrazione; aumentiamo il numero di epoche e controlliamo la convergenza dell’addestramento per applicazioni pratiche).

import numpy as np
import functools
import sklearn
import tensorflow as tf
from tensorflow import keras
import tsgm
n, n_ts, n_features = 100, 100, 20
vae_latent_dim = 8
# Load data that will be used as real
Xr, yr = tsgm.utils.gen_sine_vs_const_dataset(n, n_ts, n_features, max_value=2, const=1)
Xr = Xr.astype(np.float32)
yr = keras.utils.to_categorical(yr).astype(np.float32)
ys = yr  # use real labels as synthetic labels
# Using real data generate synthetic time series dataset
scaler = tsgm.utils.TSFeatureWiseScaler()        
scaled_data = scaler.fit_transform(Xr)
architecture = tsgm.models.zoo("cvae_conv5")(n_ts, n_features, vae_latent_dim)
encoder, decoder = architecture.encoder, architecture.decoder
vae = tsgm.models.cvae.cBetaVAE(encoder, decoder, latent_dim=vae_latent_dim, temporal=False)
vae.compile(optimizer=keras.optimizers.Adam())
# Train VAE using historical data
vae.fit(scaled_data, yr, epochs=1, batch_size=64)
Xs, ys = vae.generate(ys)
d_real = tsgm.dataset.Dataset(Xr, yr)
d_syn = tsgm.dataset.Dataset(Xs, ys)

Metrica della distanza

Per cominciare, è conveniente misurare la somiglianza tra dati reali e sintetici. Un approccio per farlo è calcolare la distanza tra un vettore di statistiche riassuntive di dati sintetici e dati reali.

Minore è la distanza, più i dati sintetici si allineano al realismo dei dati reali. Ora definiamo una serie di statistiche che serviranno come base per la nostra metrica della distanza. Metodi tsgm.metrics.statistics.axis_*_s calcolare le statistiche * sopra l’asse fornito.

statistics = (
functools.partial(tsgm.metrics.statistics.axis_max_s, axis=None),
functools.partial(tsgm.metrics.statistics.axis_min_s, axis=None),
functools.partial(tsgm.metrics.statistics.axis_max_s, axis=1),
functools.partial(tsgm.metrics.statistics.axis_min_s, axis=1))

Andando avanti, stabiliamo la metrica della distanza. Per semplicità opteremo per la norma euclidea.

discrepancy_func = lambda x, y: np.linalg.norm(x - y)

Mettendo tutto insieme, lo utilizzeremo tsgm.metrics.DistanceMetric oggetto.

dist_metric = tsgm.metrics.DistanceMetric(
statistics=statistics, discrepancy=discrepancy_func
)
print(dist_metric(d_real, d_syn))

Metrica MMD

Un approccio alternativo prevede il confronto delle distribuzioni di dati sintetici e reali. In questo contesto si rivela conveniente l’utilizzo della Massima Discrepanza Media (MMD) (3). L’MMD funge da test non parametrico a due campioni per determinare se i campioni provengono dalla stessa distribuzione. Attraverso osservazioni empiriche, abbiamo identificato la metrica MMD come un metodo particolarmente conveniente per valutare la somiglianza dei dati reali.

mmd_metric = tsgm.metrics.MMDMetric()
print(mmd_metric(Xr, Xs))

Metrica discriminativa

In questo approccio, un modello viene addestrato a distinguere tra dati reali e sintetici. Nel TSGM, tsgm.metrics.DiscriminativeMetricsi rivela uno strumento prezioso a questo scopo. Questa metrica facilita la valutazione dell’efficacia con cui un modello può discriminare tra set di dati reali e sintetici, fornendo una prospettiva aggiuntiva sulla somiglianza dei dati.

# use LSTM classification model from TSGM zoo.
model = tsgm.models.zoo("clf_cl_n")(
seq_len=Xr.shape(1), feat_dim=Xr.shape(2), output_dim=1).model
model.compile(
tf.keras.optimizers.Adam(),
tf.keras.losses.CategoricalCrossentropy(from_logits=False)
)
# use TSGM metric to measure the score
discr_metric = tsgm.metrics.DiscriminativeMetric()
print(
discr_metric(
d_hist=Xr, d_syn=Xs, model=model,
test_size=0.2, random_seed=42, n_epochs=10
)
)

Metrica di coerenza

Successivamente, passiamo alla metrica di coerenza. L’idea è in linea con scenario 1 scritto sopra. In questo caso, il nostro obiettivo è valutare la coerenza di un insieme di modelli a valle. Più in dettaglio, consideriamo un insieme di modelli ℳ, e un valutatore E: ℳ × 𝒟 → ℝ.

Per valutare la coerenza di ℳ su D e D*, misuriamo p(m₁ ∼ m₂| m₁, m₂ ∈ ℳ, D, D*) dove m₁ ∼ m₂ significa m₁ coerente con m₂: “se m₁ supera m₂ dove i modelli addestrati su D, allora avrà una performance migliore di m₂ su D* e viceversa.” La stima di questa probabilità implica fissare un insieme finito ℳ e valutare i modelli utilizzando dati reali e valutarli separatamente utilizzando dati sintetici.

In TSGM, il nostro primo passo è definire un insieme di valutatori. A questo scopo, sfrutteremo una raccolta di modelli LSTM, che vanno da uno a tre blocchi LSTM.

class EvaluatorConvLSTM():
'''
NB an oversimplified classifier, for educational purposes only.
'''
def __init__(self, model):
self._model = model
def evaluate(self, D: tsgm.dataset.Dataset, D_test: tsgm.dataset.Dataset) -> float:
X_train, y_train = D.Xy
X_test, y_test = D_test.Xy
self._model.fit(X_train, y_train)
y_pred = np.argmax(self._model.predict(X_test), 1)
print(self._model.predict(X_test).shape)
y_test = np.argmax(y_test, 1)
return sklearn.metrics.accuracy_score(y_pred, y_test)
# Define a set of models
seq_len, feat_dim, n_classes = *Xr.shape(1:), 2
models = (tsgm.models.zoo("clf_cl_n")(seq_len, feat_dim, n_classes, n_conv_lstm_blocks=i) for i in range(1, 4))
for m in models:
m.model.compile(loss='binary_crossentropy', optimizer='adam', metrics=('accuracy'))
evaluators = (EvaluatorConvLSTM(m.model) for m in models)
# Utilize the set of evaluators with ConsistencyMetric from tsgm
consistency_metric = tsgm.metrics.ConsistencyMetric(evaluators=evaluators)
print(consistency_metric(d_real, d_syn, d_real))

Esploriamo ora il modo in cui i dati generati possono contribuire a migliorare le prestazioni predittive in uno specifico problema a valle. Considereremo due approcci distinti per valutare le prestazioni a valle:

1. Aumentare i dati reali con dati sintetici.
Questo approccio si rivela prezioso quando i dati sono limitati. Integrando i dati reali con le controparti generate, miriamo a migliorare il set di addestramento per migliorare le prestazioni del modello. Consulta il nostro post sul blog sugli aumenti dei dati Qui (2).
2. Utilizzo dei dati generati esclusivamente per la formazione del modello downstream.
Negli scenari in cui i dati reali sono scarsi e privati, questo approccio entra in gioco. In questo caso, il modello downstream viene addestrato esclusivamente sui dati generati e successivamente valutato su dati reali.

downstream_model = tsgm.models.zoo("clf_cl_n")(seq_len, feat_dim, n_classes, n_conv_lstm_blocks=1).model
downstream_model.compile(loss='binary_crossentropy', optimizer='adam', metrics=('accuracy'))
evaluator = EvaluatorConvLSTM(downstream_model)
downstream_perf_metric = tsgm.metrics.DownstreamPerformanceMetric(evaluator)
print(downstream_perf_metric(d_real, d_syn, d_real))

Il risultato indica un guadagno di precisione derivante dall’aumento con dati sintetici rispetto al modello addestrato esclusivamente sui dati di addestramento.

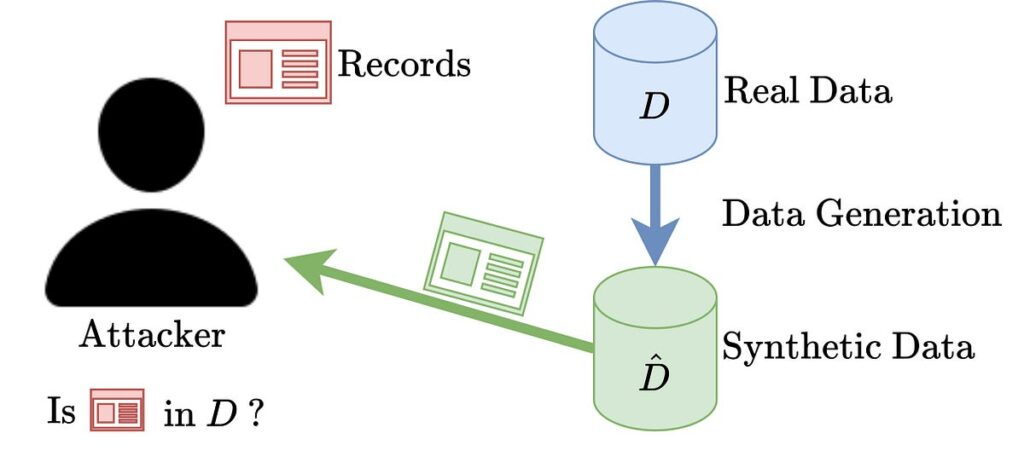
Un approccio per misurare la privacy dei dati sintetici è misurare la suscettibilità agli attacchi di inferenza di appartenenza. La procedura di attacco tramite inferenza sull’appartenenza è rappresentata visivamente nella figura sopra. L’idea è la seguente. Immagina un utente malintenzionato che abbia accesso a dati sintetici e a un particolare campione di dati (che potrebbe esistere o meno nel set di dati originale). L’obiettivo è **dedurre** se questo campione è presente nei dati reali.

“tsgm.metrics.PrivacyMembershipInferenceMetric” misura la suscettibilità agli attacchi di inferenza di appartenenza utilizzando dati sintetici. La procedura di valutazione passo passo è delineata come segue:
1. Suddivisione dei dati. Suddividere i dati storici in set di training e hold-out (indicati come Dₜ e Dₕ),
2. Formazione sul modello generativo. Addestra un modello generativo su Dₜ e genera un set di dati sintetico D*,
3. Formazione sul modello di classificazione a una classe (OCC). Addestrare un modello di classificazione a una classe (OCC) sui dati sintetici D* e valutarlo su Dₜ e Dₕ,
4. Calcolo del punteggio obiettivo. Utilizzare uno meno la precisione del modello OCC come punteggio target.

Questo processo di valutazione fornisce informazioni sulla potenziale vulnerabilità agli attacchi di inferenza sull’appartenenza che sfruttano i dati sintetici.

Introduciamo ora un modello di attaccante. A scopo dimostrativo, definiremo un classificatore SVM a una classe.

class FlattenTSOneClassSVM:
def __init__(self, clf):
self._clf = clf
def fit(self, X):
X_fl = X.reshape(X.shape(0), -1)
self._clf.fit(X_fl)
def predict(self, X):
X_fl = X.reshape(X.shape(0), -1)
return self._clf.predict(X_fl)
attacker = FlattenTSOneClassSVM(sklearn.svm.OneClassSVM())
privacy_metric = tsgm.metrics.PrivacyMembershipInferenceMetric(
attacker=attacker
)

Ora definiamo un set di test e misuriamo la metrica della privacy:

X_test, y_test = tsgm.utils.gen_sine_vs_const_dataset(10, 100, 20, max_value=2, const=1)
d_test = tsgm.dataset.Dataset(X_test, keras.utils.to_categorical(y_test))
# 1 indicates high privacy and 0 -- low privacy.
privacy_metric(d_real, d_syn, d_test)

Con questa metrica, il nostro obiettivo è quantificare la diversità dei dati sintetici. Considera l’immagine qui sotto, dove i punti rossi rappresentano i dati reali e i punti blu indicano i dati sintetici. Quale opzione produce un set di dati sintetico superiore? Quello a destra appare più favorevole, ma perché? La risposta sta nella sua diversità, che lo rende potenzialmente più versatile e utile. Tuttavia, la diversità da sola non è sufficiente; è fondamentale considerare altri parametri insieme, come la distanza o le prestazioni a valle. Nella nostra esplorazione, esemplificheremo il concetto utilizzando l’entropia.

spec_entropy = tsgm.metrics.EntropyMetric()
print(spec_entropy(Xr))
print(spec_entropy(Xs))

Il tema dell’equità si interseca con la generazione di serie temporali sintetiche in due modi significativi. In primo luogo, è fondamentale valutare se i dati sintetici introducono nuovi bias. In secondo luogo, i dati sintetici offrono l’opportunità di mitigare i pregiudizi inerenti ai dati originali. Definire procedure standardizzate per verificare l’equità si rivela impegnativa, poiché spesso dipende dalle specificità dei problemi a valle. Alcuni parametri illustrativi per misurare l’equità comprendono la parità demografica, i paradigmi di parità tariffaria predittiva e le pari opportunità.

Prendiamo, ad esempio, le pari opportunità. L’uguaglianza di opportunità funge da metrica di equità progettata per valutare se, per un’etichetta preferita (quella che conferisce un vantaggio o beneficio a una persona) e un dato attributo, un classificatore prevede quell’etichetta preferita ugualmente bene per tutti i valori di quell’attributo (6 ). Questa metrica è determinante per garantire imparzialità e parità di trattamento tra i diversi valori degli attributi. Un ottimo esempio di questa metrica è fornito in (6): “Supponiamo che l’Università di Glubbdubdrib ammetta sia i lillipuziani che i Brobdingnagiani a un rigoroso programma di matematica. Le scuole secondarie dei lillipuziani offrono un ricco curriculum di lezioni di matematica e la stragrande maggioranza degli studenti è qualificata per il programma universitario. Le scuole secondarie di Brobdingnagians non offrono affatto lezioni di matematica e, di conseguenza, molti meno studenti sono qualificati. Le pari opportunità sono soddisfatte per l’etichetta preferita di “ammesso” rispetto alla nazionalità (lillipuziano o brobdingnagiano) se gli studenti qualificati hanno le stesse probabilità di essere ammessi indipendentemente dal fatto che siano lillipuziani o brobdingnagiani.”

Per valutare qualitativamente i dati è conveniente:
UN. disegnare campioni e visualizzare singoli campioni da dati sintetici e reali,
B. costruire incorporamenti dei campioni generati e visualizzarli utilizzando, ad esempio, TSNE. Esemplifichiamo (b) con TSGM:

tsgm.utils.visualize_tsne_unlabeled(Xr, Xs, perplexity=10, markersize=20, alpha=0.5)

Questo post sul blog fa parte del progetto TSGM, in cui stiamo creando uno strumento per migliorare le pipeline di serie temporali tramite l’aumento e la generazione di dati sintetici. Se lo hai trovato utile, dai un’occhiata al nostro repository e valuta la possibilità di citare l’articolo su TSGM:

@article{
nikitin2023tsgm,
title={TSGM: A Flexible Framework for Generative Modeling of Synthetic Time Series},
author={Nikitin, Alexander and Iannucci, Letizia and Kaski, Samuel},
journal={arXiv preprint arXiv:2305.11567},
year={2023}
}

In conclusione, abbiamo esplorato varie tecniche di valutazione per i dati di serie temporali sintetiche, fornendo una panoramica completa di diversi scenari. Per navigare in modo efficace attraverso questi metodi, è utile considerare gli scenari descritti. In definitiva, la scelta della metrica giusta dipende dal problema a valle, dall’area di applicazione e dalle norme legali che regolano i dati in uso. L’insieme diversificato di metriche fornite mira ad assistere nella creazione di una pipeline di valutazione completa su misura per il tuo problema specifico.

(1) Nikitin, A., Iannucci, L. e Kaski, S., 2023. TSGM: Un quadro flessibile per la modellazione generativa di serie temporali sintetiche. arXiv prestampa arXiv:2305.11567. Link Arxiv.
(2) Miglioramenti delle serie temporali, post TowardsDataScience, https://medium.com/towards-data-science/time-series-augmentations-16237134b29b.
(3) Gretton, A., Borgwardt, KM, Rasch, MJ, Schölkopf, B. e Smola, A., 2012. Un test del kernel su due campioni. The Journal of Machine Learning Research, 13(1), pp.723–773. Collegamento JMLR.
(4) Wen, Q., Sun, L., Yang, F., Song, X., Gao, J., Wang, X. e Xu, H., 2020. Time series data augmentation for deep learning: A Survey . arXiv prestampa arXiv:2002.12478. Link Arxiv.
(5) Wattenberg, M., Viégas, F. e Hardt, M., 2016. Attaccare la discriminazione con un apprendimento automatico più intelligente. Ricerca Google, 17. Collegamento alla ricerca di Google.
(6) Glossario dell’apprendimento automatico: equità. Blog degli sviluppatori di Google.
Collegamento al blog degli sviluppatori di Google.