Sbloccare intuizioni visive in un ramo difficile ma potente della matematica
Oggi stavo diluviando Variabili complesse e funzioni analitiche dagli stimati Fornberg e Piret, facendo del mio meglio per comprendere come si comportano le funzioni con valori complessi. Visualizzare mentalmente tali funzioni è estremamente difficile poiché accettano un input reale e uno immaginario e generano anche due componenti. Pertanto, un singolo grafico 3D non è sufficiente per vedere come si comporta la funzione. Piuttosto, dobbiamo dividere tale visualizzazione in trame separate delle parti immaginarie e reali, o in alternativa per grandezza e argomento, o angolo.
Volevo poter giocare con qualsiasi funzione mi venisse in mente, trascinare e ingrandire le sue trame ed esplorarla in dettaglio visivo per capire come risultava dall’equazione. Per tale compito, Wolfram Mathematica è un eccellente strumento di partenza.
plotComplexFunction(f_):=Module({z,rePlot,imPlot,magPlot,phasePlot},z=x+I y;rePlot = Plot3D(Re(f(z)),{x,-2,2},{y,-2,2},AxesLabel->{"Re(z)","Im(z)","Re(f(z))"},Mesh->None);
imPlot = Plot3D(Im(f(z)),{x,-2,2},{y,-2,2},
AxesLabel->{"Re(z)","Im(z)","Im(f(z))"},
Mesh->None);
magPlot = Plot3D(Abs(f(z)), {x, -2, 2}, {y, -2, 2},
AxesLabel -> {"Re(z)", "Im(z)", "Abs(f(z))"},
Mesh -> None,
ColorFunction -> Function({x, y, z}, ColorData("Rainbow")(Rescale(Arg(x + I y), {-Pi, Pi}))),
ColorFunctionScaling -> False);
phasePlot=DensityPlot(Arg(f(z)),{x,-2,2},{y,-2,2},
ColorFunction->"Rainbow",
PlotLegends->Automatic,
AxesLabel->{"Re(z)","Im(z)"},
PlotLabel->"Phase");
GraphicsGrid({{rePlot,imPlot},{magPlot,phasePlot}},ImageSize->800));
f(z_):=(1/2)*(z+1/z);
plotComplexFunction(f)
https://github.com/dreamchef/complex-functions-visualization
https://github.com/dreamchef/complex-functions-visualization
Ho scritto il codice Mathematica sopra per produrre una griglia di grafici che mostrano la funzione in entrambi i modi appena descritti. In alto, la parte immaginaria e quella reale della funzione
sono mostrati, e in basso, e la magnitudine, e la fase mostrata a colori:
Dopo aver giocato con alcune funzioni utilizzando questo codice ed essermi convinto che avessero senso, ero interessato a ottenere la stessa funzionalità in Python, per collegarla agli altri miei progetti di programmazione matematica.
Ho trovato un eccellente progetto su GitHub (https://github.com/artmenlope/complex-plotting-tools) che ho deciso di utilizzare come punto di partenza e a cui potenzialmente contribuire in futuro. Il repository ha fornito un’interfaccia molto semplice per tracciare funzioni con valori complessi in vari modi. Grazie https://github.com/artmenlope! Ad esempio, dopo l’importazione numpy, matplotlibe i pronti contro termine cplotting_tools modulo che definisce la funzione e la chiamata cplt.complex_plot3D(x,y,f,log_mode=False) produce quanto segue:
Questi sono tutti per la stessa f(z) di cui sopra. Per visualizzare le parti immaginarie e reali affiancate della funzione, utilizzare cplot.plot_re_im(x,y,f,camp="twilight",contour=False,alpha=0.9:
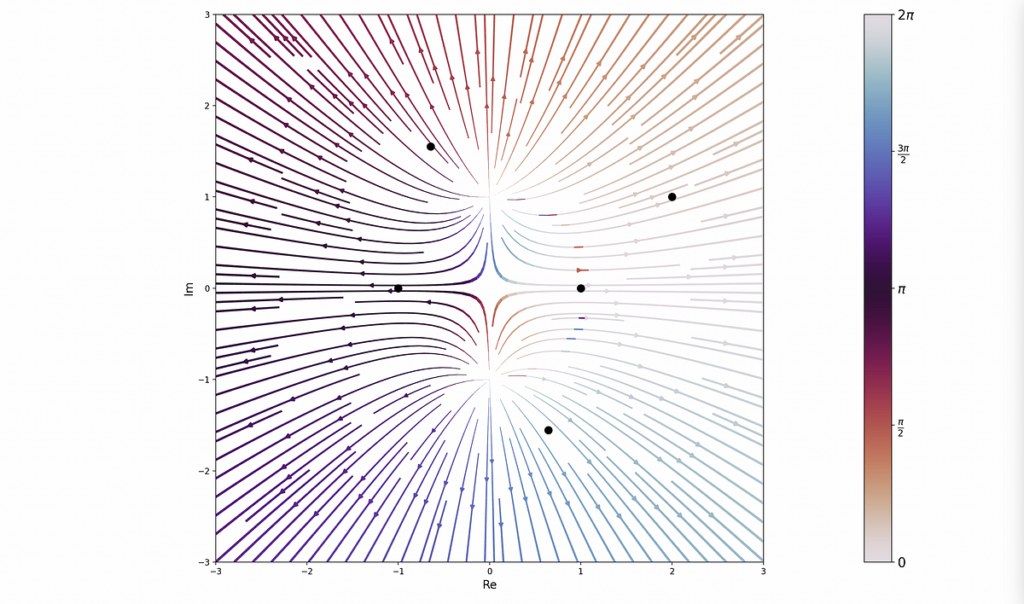
Inoltre, la libreria fornisce altri modi interessanti per studiare le funzioni, incluso un diagramma del flusso:
La libreria mostra molte promesse ed è relativamente facile da usare! Richiede a pts variabile da definire che codifica i poli e gli zeri della funzione data. Wolfram non lo richiede perché calcola le posizioni di questi punti sotto il cofano. Farebbe risparmiare molto sforzo all’utente se anche gli strumenti di disegno complessi avessero questa funzionalità. Ho intenzione di implementarlo nel modulo nel prossimo futuro.
Nel frattempo, divertiti a progettare con Wolfram e Python e inviami qualsiasi domanda o idea di sviluppo.
Saluti!
Dani
Se non diversamente specificato, tutte le immagini sono state create dall’autore.
Fonte: towardsdatascience.com
