Algebra lineare 4: Equazioni matriciali | di tenzin migmar (t9nz) | Novembre 2023 | Intelligenza-Artificiale

Risolvere equazioni di matrice Ax= b

Prefazione

Bentornati alla quarta edizione della mia serie in corso sulle basi dell’algebra lineare, la matematica fondamentale dietro l’apprendimento automatico. Nel mio precedente articoloHo introdotto i vettori, le combinazioni lineari e gli span vettoriali. Questo saggio esaminerà l’equazione della matrice UNx = B e vedremo come il principio stesso della risoluzione di un sistema di equazioni lineari sia legato all’equazione di matrice.

Questo articolo sarebbe più utile ai lettori se letto insieme a Algebra lineare e le sue applicazioni di David C. Lay, Steven R. Lay e Judi J. McDonald. Considera questa serie come una risorsa complementare.

Sentiti libero di condividere pensieri, domande e critiche.

L’intuizione

L’ultima volta che abbiamo interrotto lo studio delle combinazioni lineari che avevo promesso avrebbero avuto importanti implicazioni. Ricordiamo che dati i vettori v₁, v₂, … vₐ in ℝⁿ e gli scalari (noti anche come pesi) c₁, c₂, … cₐ, il combinazione lineare è il vettore definito dalla somma dei multipli scalari, c₁v₁ + c₂v₂ + … + cₐvₐ.¹

Diciamo che un vettore B è una combinazione lineare di un insieme di vettori v₁, v₂, .. vₐₚ in Rⁿ, se esiste un insieme di pesi c₁, c₂, … cₐ (una soluzione) tale che c₁v₁ + c₂v₂ + … + cₐvₐ = B.

Per determinare se B è una combinazione lineare di alcuni vettori dati v₁, v₂, .. vₐ abbiamo organizzato i nostri vettori in un sistema di equazioni lineari, quindi abbiamo creato una matrice aumentata delle nostre equazioni e abbiamo utilizzato operazioni di riduzione delle righe per ridurre la matrice alla forma a scaglioni ridotti. Se la forma a scaglioni ridotti della riga avesse un’incoerenza, cioè una riga che assomigliasse a questa: (0, 0, … | M) Dove M ≠ 0, ciò significava che il nostro vettore B non è una combinazione lineare dei vettori perché non esiste un insieme di pesi per l’equazione c₁v₁ + c₂v₂ + … + cₐvₐ = B A valere.

Se non esistesse tale incoerenza, ciò significava che avremmo potuto scrivere il vettore b come una combinazione lineare di un insieme di vettori, come nell’esempio sopra. Ricordi come abbiamo verificato la nostra risposta alla fine? Moltiplicheremo ciascun vettore per il rispettivo scalare e poi troveremo la somma dei vettori. Se la somma vettoriale è uguale a Bsapevamo di aver fatto correttamente i nostri calcoli e questo B era infatti una combinazione lineare.

Questo processo di verifica è l’equazione di matrice UNx = B sotto mentite spoglie!

Ascia = b

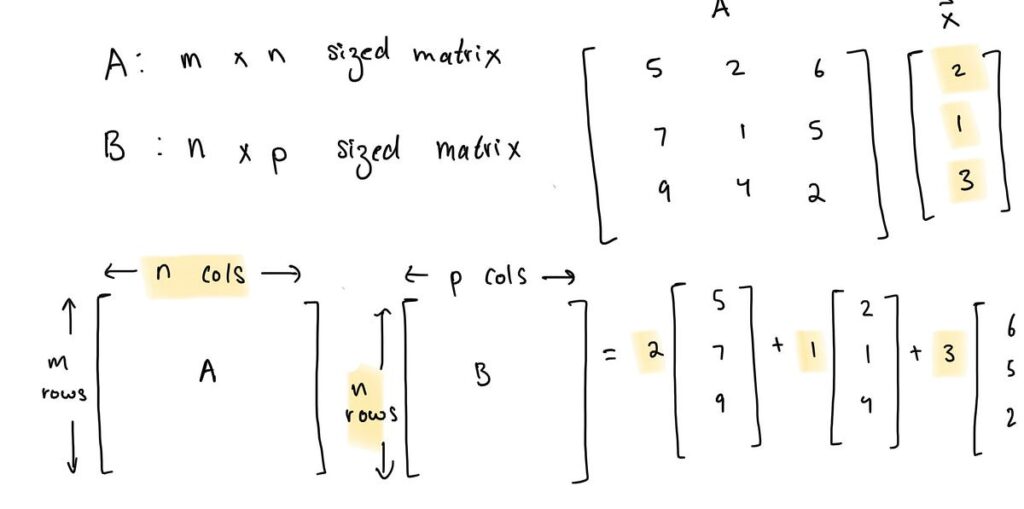
Se UN è un M X N matrice e x è in Rⁿ (vedrai perché è importante che x sia in Rⁿ nella sezione successiva), quindi il prodotto UNx è la combinazione lineare dei vettori (colonne) in UNutilizzando i corrispondenti scalari in x.

Si noti che niente di tutto questo è materiale nuovo, lo abbiamo già calcolato inconsapevolmente UNx durante la verifica delle nostre combinazioni lineari nel mio articolo precedente. IL UNx = B l’equazione di matrice è comunque fondamentale perché formalizza tutto questo in una notazione compatta e riaffiorerà in seguito in modi nuovi.

Ora sappiamo che se ci viene dato un file M X N matrice UN ex e calcoliamo il prodotto della matrice UNx ed è uguale a BPoi B può essere scritto come una combinazione lineare dei vettori (colonne) in A e degli scalari/voci in x. Quindi in sintesi: l’equazione UNx = B avrà soluzione (x) solo se b può essere scritto come combinazione lineare delle colonne di A.

Moltiplicazione di matrici

Mi sono presentato UNx = B come prodotto di matrici, ma non ho ancora spiegato la moltiplicazione di matrici (che è cosa UNx è)!

Moltiplicazione di matrici è l’operazione di moltiplicare due matrici per produrne una, il loro prodotto. Abbiamo già visto l’addizione di matrici in cui due matrici vengono sommate per produrre la loro somma. Per poter definire l’addizione di matrici, le due matrici che vengono aggiunte, matrice A e matrice B, devono avere la stessa dimensione. Allo stesso modo, anche la moltiplicazione di matrici ha un requisito. Per moltiplicare la matrice UN e matrice B e produrre ABil numero di colonne nella matrice UN deve essere uguale al numero di righe nella matrice B. La dimensione del prodotto di matrice UN E Bche chiameremo matrice C dipenderà dal numero di righe nella matrice UN e numero di colonne nella matrice B. Matrice C avrà m (# di righe nella matrice UN) righe e p (n. di colonne nella matrice B) colonne.

Quindi, come funziona la moltiplicazione di matrici? Se dovessimo moltiplicare la matrice A e B, ciascuna delle voci della riga i-esima e della colonna j-esima nel prodotto della matrice è la prodotto scalare della riga i-esima nella matrice A e della riga j-esima nella matrice B.

Per ora, tutto quello che devi sapere è che il prodotto scalare è la somma del prodotto delle voci corrispondenti tra due vettori e si definisce solo quando i due vettori hanno lo stesso numero di voci. Questa spiegazione è lungi dal rendere giustizia al prodotto scalare, ma conserverò l’intera intuizione geometrica per dopo.

Per brevità, ho calcolato il prodotto matriciale di due matrici 2 x 2, ma la stessa procedura si generalizza per matrici di qualsiasi dimensione purché le matrici soddisfino i criteri per la moltiplicazione delle matrici, altrimenti il ​​loro prodotto sarà indefinito.

Proprietà della Moltiplicazione di Matrici

Se UN, B E C Sono N X N matrici e C E D sono scalari, allora sono vere le seguenti proprietà.³

1. AB ≠ BA (non commutativo in generale)
2. (AB)C = A(BC) (associativo)
3. A(B+C) = AB + AC e (B+C)A = BA + CA (distributivo)
4. 0A = 0 (proprietà moltiplicativa di zero)

Fai attenzione a notare che la moltiplicazione di matrici non è commutativa, questa proprietà potrebbe richiedere del tempo per essere mantenuta dato che siamo intuitivamente abituati alla commutatività con i numeri reali.

Queste proprietà sono utili per il calcolo dei prodotti di matrici, che sarà un argomento ricorrente in tutta l’Algebra Lineare.

Conclusione

La moltiplicazione della matrice è un’operazione matematica fondamentale che è alla base della funzionalità principale delle reti neurali, in particolare nelle fasi di propagazione feedforward e back.

Nella fase feedforward di una rete neurale, i dati vengono elaborati attraverso i suoi vari strati e la moltiplicazione delle matrici è al centro di questa operazione. Ogni strato di una rete neurale è composto da neuroni, rappresentati come somme ponderate degli input, seguite da una funzione di attivazione. Queste somme ponderate vengono calcolate utilizzando la moltiplicazione di matrici.

Durante il passaggio di propagazione all’indietro, la rete neurale impara dai propri errori. Regola i pesi dei neuroni per ridurre al minimo l’errore tra gli output previsti e quelli effettivi. La moltiplicazione della matrice è ancora una volta una componente chiave di questo processo, in particolare nel calcolo dei gradienti, che indicano quanto ciascun peso dovrebbe essere modificato per ridurre al minimo l’errore.

Imparare la matematica è un’impresa entusiasmante esclusivamente per i suoi meriti, ma apprendere le applicazioni dell’algebra lineare insieme alla teoria può rendere il viaggio lungo una ripida curva di apprendimento ancora più stimolante.

Riepilogo

In questo capitolo abbiamo appreso:

• L’intuizione dietro le combinazioni lineari e il prodotto matriciale UNx = B: come il prodotto matrice non è necessariamente un concetto nuovo, ma che formalizza una procedura che già utilizzavamo!
• UNx = B: il prodotto della matrice ha una soluzione x se B è una combinazione lineare dell’insieme di vettori (colonne) in UN.
• Moltiplicazione di matrici: l’operazione alla base UNx = B che è ampiamente utilizzato nelle applicazioni di apprendimento automatico, esempi specifici includono le reti neurali.
• Proprietà della moltiplicazione delle matrici: non commutatività, associatività, proprietà distributiva e moltiplicativa dello zero.

Appunti

*Tutte le immagini create dall’autore se non diversamente specificato.
*Mi scuso per aver impiegato un po’ di tempo per continuare da dove avevamo interrotto l’ultima volta. Attualmente sto sostenendo gli esami intermedi (incluso uno di Algebra lineare ahah!)
¹Definizione di combinazioni lineari a cui si fa riferimento da Algebra lineare e sue applicazioni 6a edizione di David C. Lay, Steven R. Lay e Judi J. McDonald
²Definizione per le proprietà del prodotto matriciale a cui si fa riferimento da Algebra lineare e sue applicazioni 6a edizione di David C. Lay, Steven R. Lay e Judi J. McDonald
³Proprietà della matrice a cui si fa riferimento src.